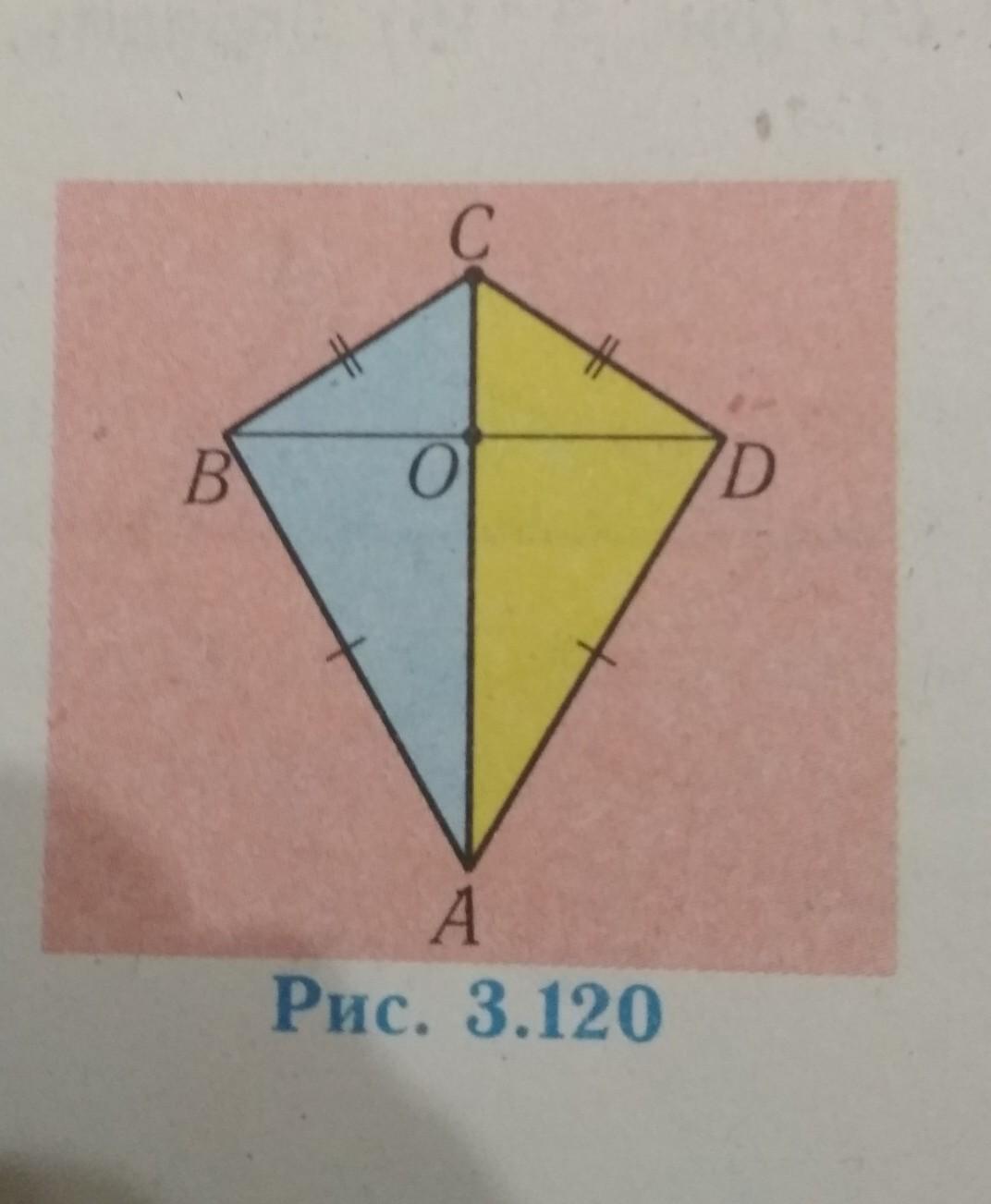
ЖП ПОМОГИТЕ ДАМ 60 БАЛОВ 388. Дано: AB = AD, BC = CD . Доведіть, що BAO = DAO, Bco = DCO, BO = OD, AC I BD. (Rus) Дано: AB = AD, BC = CD . Докажите, что BAO = DAO, Bco = DCO, BO = OD, AC I BD.​

Ответ:

1. Треугольник ABC равен тр-ку ADC (по 3-му признаку):

а) AB = AD - по условию;

б) BC = CD - по условию;

в) сторона AC - общая.

Значит, ∠BAO = ∠DAO.

2. ΔABO = ΔADO (по 1-му признаку):

а) AB = AD - по условию

б) AO - общая

в) ∠BAO = ∠DAO - по доказанному в п.1

3. Из равенства ΔABO и ΔADO вытекает равенство углов ∠BOA и ∠DOA. Также по условию задачи ∠BOA + ∠DOA = 180°, поэтому ∠BOA = ∠DOA = 90°. Следовательно AC⊥BD, что и требовалось доказать.