СРОЧНО ПОЖАЛУЙСТА ПОМОГИТЕ!!! Заранее благодарю!
При каких значениях параметра а квадратное уравнение

x2 - 2(a + 3)x + 5a - 9 = 0

не имеет решений

Ответ: а є (2;9)

Пошаговое объяснение: что бы уравнение не имело корней нужно что бы дискриминант был меньше нуля

формула дискриминанта в нашем случае будет

Значит приравниваем

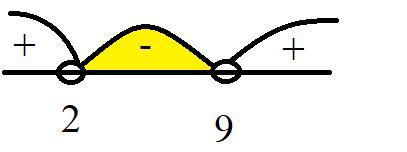
рисуем диапазон и видим что при 2<a<9 дискриминант будет меньше 0, а значит уравнение не будет иметь корней