Ответы
Ответ дал:
1
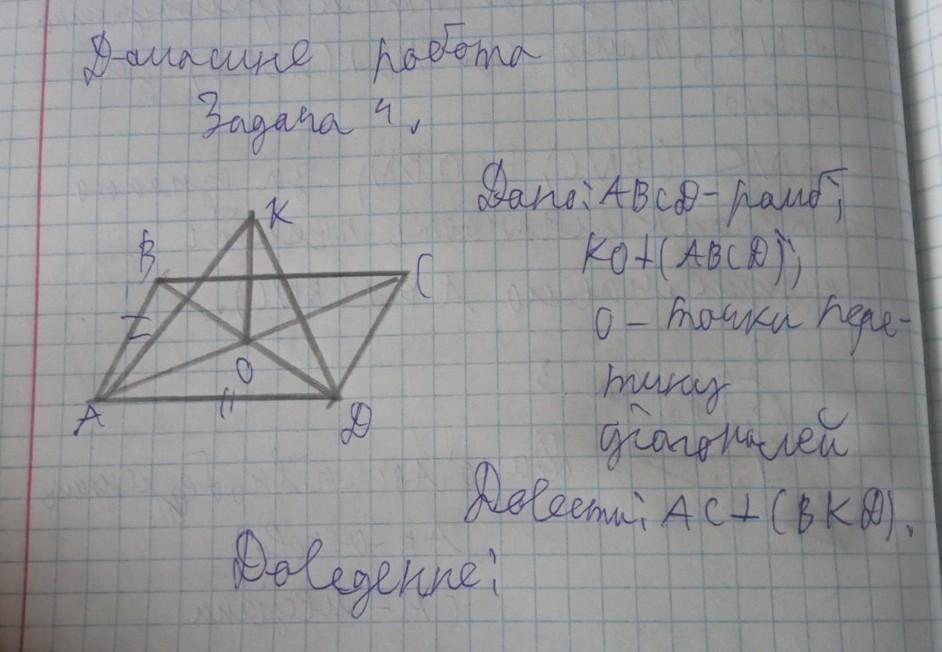
Вспомним признак перпендикулярности прямой и плоскости: если прямая перпендикулярна двум пересекающимся прямым, лежащим в данной плоскости, то прямая перпендикулярна всей плоскости. По свойству ромба диагональ AC перпендикулярна диагонали BD, которая ещё и лежит в плоскости BKD, одна прямая есть. В плоскости BKD есть прямая KO, которая перпендикулярна всей плоскости ABC, а значит и перпендикулярна прямой AC. Мы получили, что AC перпендикулярна BD и KO, BD и KO лежат в плоскости BKD, а также пересекаются в точке О, из всего вышесказанного следует, что АС перпендикулярна плоскости BKD, что и требовалось доказать
Похожие вопросы
1 год назад
1 год назад
2 года назад
2 года назад
8 лет назад
9 лет назад