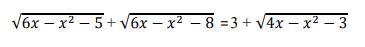Решите уравнение (100 баллов)

ОДЗ:

6x-x^2-5=0⇒x^2-6x+5=0  

D=36-20=16

x=(6±4)/2

x^2-6x+5=(x-1)(x-5)

6x-x^2-5≥0   ⇒x^2-6x+5≤0  ⇒(x-1)(x-5)≤0 ⇒x∈[1;5]

6x-x^2-8=0⇒x^2-6x+8=0  

D=36-32=4

x=(6±2)/2

x^2-6x+8=(x-2)(x-4)

6x-x^2-8≥0   ⇒x^2-6x+8≤0  ⇒(x-2)(x-4)≤0 ⇒x∈[2;4]

4x-x^2-3=0⇒x^2-4x+3=0  

D=16-12=4

x=(4±2)/2

x^2-4x+3=(x-1)(x-3)

4x-x^2-3≥0   ⇒x^2-4x+3≤0  ⇒(x-1)(x-3)≤0 ⇒x∈[1;3]

ОДЗ:

Оценка левой части уравнения на ОДЗ:

√3≤√ (6x-x^2-5) +√ (6x-x^2-8)≤3.

Наибольшее  значение равно 3

Оценка правой части уравнения на ОДЗ:

3≤3+√ (4x-x^2-3)

Наименьшее  значение  равно 3

Значение общее решение уравнения возможно лишь при

3+√ (4x-x^2-3) =3

√ (4x-x^2-3) =0

x=1 или x=3

x=1 не принадлежит ОДЗ.

О т в е т. х=3 - единственный корень уравнения