алгебра алгебра алгебра алгебра алгебра алгебра алгебра алгебра алгебра алгебра алгебра алгебра алгебра алгебра алгебра алгебра алгебра алгебра алгебра алгебра алгебра алгебра алгебра алгебра алгебра алгебра алгебра алгебра

Приложения:

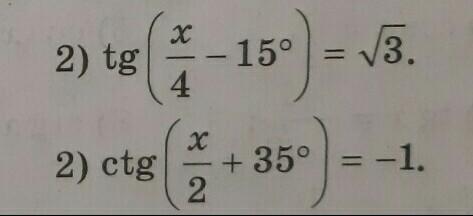
Ответы

Ответ дал: bertramjeratire

Ответ:

$\tan( \frac{x}{3} - {15}^{ \circ} ) = \sqrt{3}$

ОДЗ:

$\frac{x}{4} - {15}^{ \circ} ≠ \frac{\pi}{2} + k\pi \: \: \: \: \: \: \:k \in \Z$

Переведем 15° в радианы

${15}^{ \circ} \times \frac{\pi}{ {180}^{ \circ} } = \frac{\pi}{12}$

$\frac{x}{4}≠ \frac{\pi}{2} + \frac{\pi}{12} + k\pi \: \: \: \: \: \: \: \:k \in \Z \\ \frac{x}{4} ≠ \frac{7\pi}{12} + k\pi \: \: \: \: \: \: \: \: k \in \Z\\ x ≠ \frac{7\pi}{3} + k\pi \: \: \: \: \: \: \: k \in \Z$

Теперь решаем

$\frac{x}{4} - \frac{\pi}{12} = \arctan( \sqrt{3} ) \\ \frac{x}{4} - \frac{\pi}{12} = \frac{\pi}{3} + k\pi \: \: \: \: \: k \in \Z \\ 3x - \pi = 4\pi + 12k\pi \: \: \: \: \: \: k \in \Z \\ 3x = 5\pi + 12k\pi \: \: \: \: \: k \in \Z \\ x = \frac{5\pi}{3} + 4k\pi \: \: \: \: k \in \Z$