Геометрія помогите пжжжж

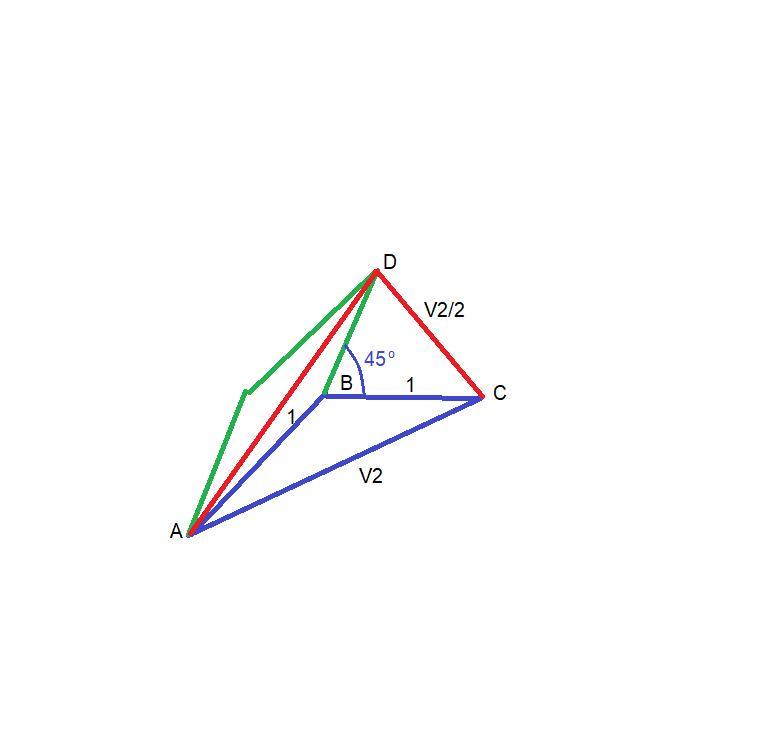
Примем длины катетов заданного треугольника за 1.

То есть: АВ = ВС = 1, гипотенуза АС = √2.

Пусть через катет АВ проходит плоскость, составляющая угол 45 градусов с плоскостью АВС.

Треугольник ABD - это проекция АВС на эту плоскость.

Отсюда сразу понятен угол между вторым катетом и плоскостью ABD - он равен 45 градусов.

Найдём длину AD:

AD = √(1² + (√2/2)²) = √(1 + (2/4)) = √(6/4) = √(3/2).

Применим теорему косинусов для определения угла A между гипотенузой АС и плоскостью ABD.

cos(A) = ((√(3/2))² + (√2)²) - (√2/2)²)/(2*(√(3/2))*√2) = √3/2.

Угол равен arccos(√3/2) = 30 градусов.