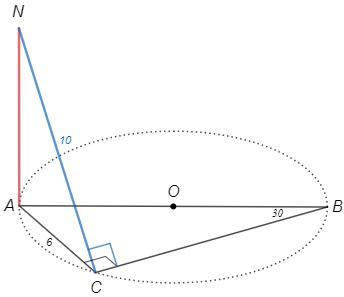
Дана окружность с центром в точке О и радиусом 6. Отрезок AB - диаметр окружности, а отрезок BC - хорда. Угол ABC равен 30 градусов. Отрезок АN перпендикуляр к плоскости окружности. Найди расстояние от точки N до плоскости окружности, если расстояние от точки N до прямой BC равно 10​

AB=2R=12 (диаметр)

∠ACB=90° (вписанный угол, опирающийся на диаметр)

AC=AB/2 =6 (катет против угла 30°)

NA⊥(ABC), AC⊥BC => NC⊥BC (т о трех перпендикулярах)

Расстояние от точки до прямой - длина перпендикуляра.

NC=10 (расстояние от точки N до прямой BC)

NA⊥(ABC) => NA⊥AC, ∠NAC=90°

Расстояние от точки до плоскости - длина перпендикуляра.

NA=√(NC^2-AC^2) =8 (т Пифагора)