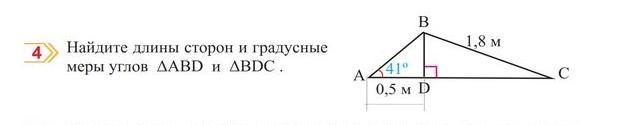???????????????????????

Пошаговое объяснение:

Дано: ∆ABC; BD_|_AC

уг.А = 41°; ВС = 1,8м, АD =0,5м.

Найти: стороны и углы ∆ABD, ∆CBD

Решение:

BD_|_AC => уг.ADB = уг.CDB = 90°

Рассмотрим ∆ABD.

уг.D = 90°, AD = 0,5 m, уг.A = 41°.

=> уг.ABD = 180 - уг.D - уг.A = 180 - 90 - 41

уг.ABD = 49°

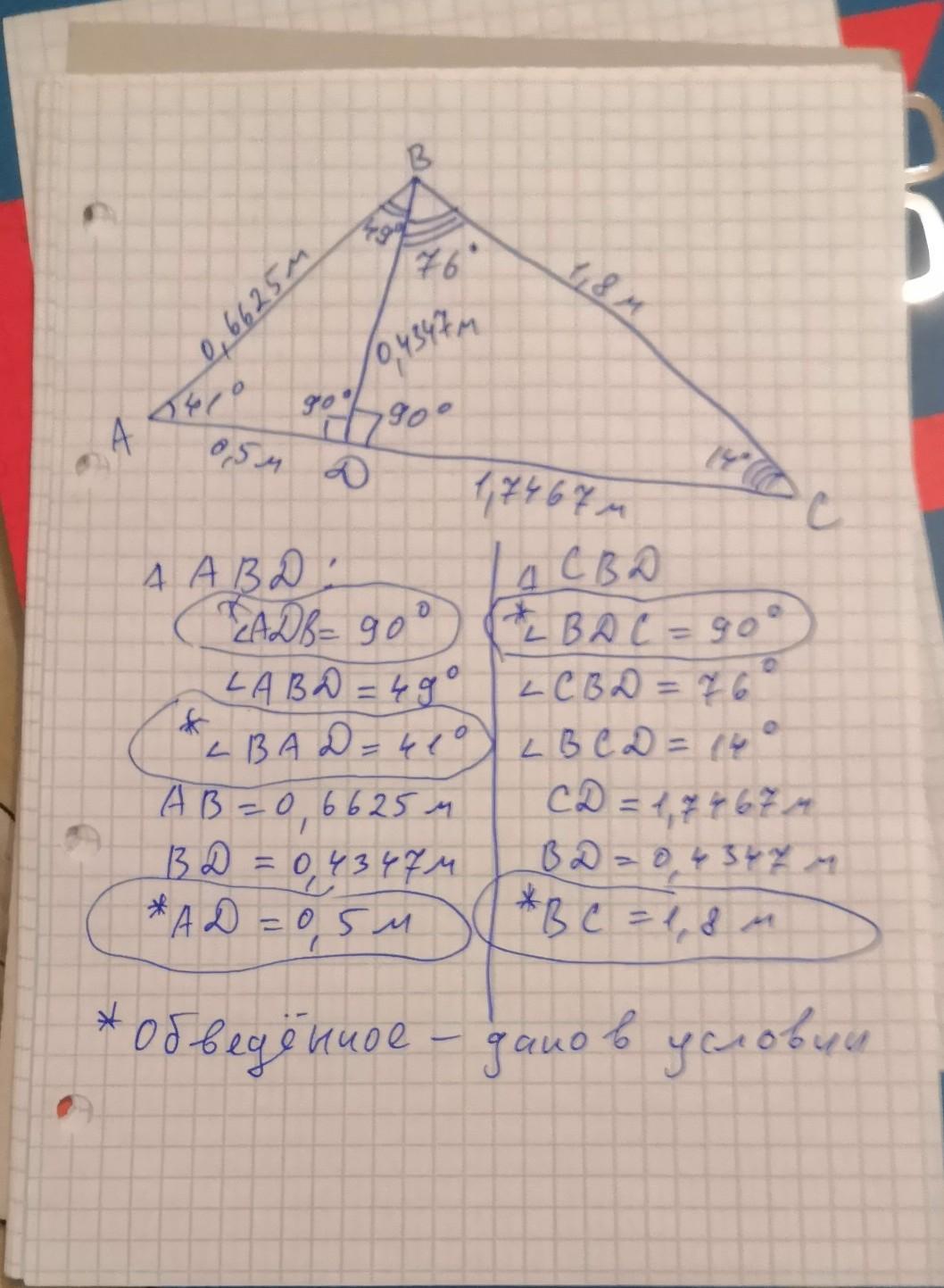
Итак, мы нашли: Для ∆АВD:

AB = 0,6625 m, AD = 0,5 m, BD = 0,4347 m

Рассмотрим ∆CDB:

По Т. Пифагора:

Далее, найдем уг.С

А Отсюда найдем и уг.DBC:

Вот и все. Все требуемые величины определены.

Общий ответ - см. на рис.