< >

х5+х4-3х3-3х2-х-1=0 решение

Ответы

Ответ дал: balakine977

Ответ:

$-\sqrt{\frac{3+\sqrt{13} }{2} }; -1; \sqrt{\frac{3+\sqrt{13} }{2} }$

Пошаговое объяснение:

Заметим, что x = -1 - корень уравнения:

$(-1)^5 + (-1)^4 - 3*(-1)^3 - 3*(-1)^2 -(-1)-1 = 0$

По следствию из т. Безу, это означает, что многочлен из левой части уравнения делится на (x+1).

Поделив исходный многочлен на (x+1), получаем $x^4-3x^2-1$ (см. фото), т. е. $x^5+x^4-3x^3-3x^2-x-1 = (x+1)(x^4-3x^2-1) = 0$

$(x+1)(x^4-3x^2-1) = 0$ ⇔ $x+1 = 0$ или $x^4-3x^2-1 = 0$

Первое уравнение, очевидно, имеет решение x = -1, а второе решим, заменив x^2 на y. Тогда:

$y^2-3y-1 = 0$

$D = 9 + 4 = 13; \sqrt{D} = \sqrt{13}\\y_1 = \frac{3+\sqrt{13}}{2}\\ y_2 = \frac{3-\sqrt{13}}{2}$

Вспомнив, что y = x^2, понятно, что y ≥ 0. Но $\frac{3-\sqrt{13} }{2} < 0$ , т. е. $y_2 \neq x^2$

$x^2 = \frac{3+\sqrt{13} }{2}$ , откуда $x = \pm\sqrt{\frac{3+\sqrt{13} }{2} }$

Ответ: $-\sqrt{\frac{3+\sqrt{13} }{2} }; -1; \sqrt{\frac{3+\sqrt{13} }{2} }$

Приложения:

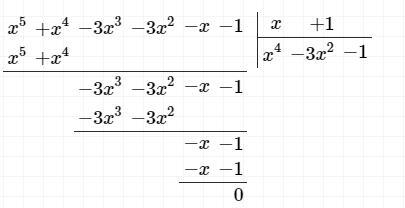
Похожие вопросы

Математика

1 год назад

Физика

1 год назад

История

2 года назад

Русский язык

2 года назад

История

8 лет назад

Математика

8 лет назад

Математика

9 лет назад

Математика

9 лет назад