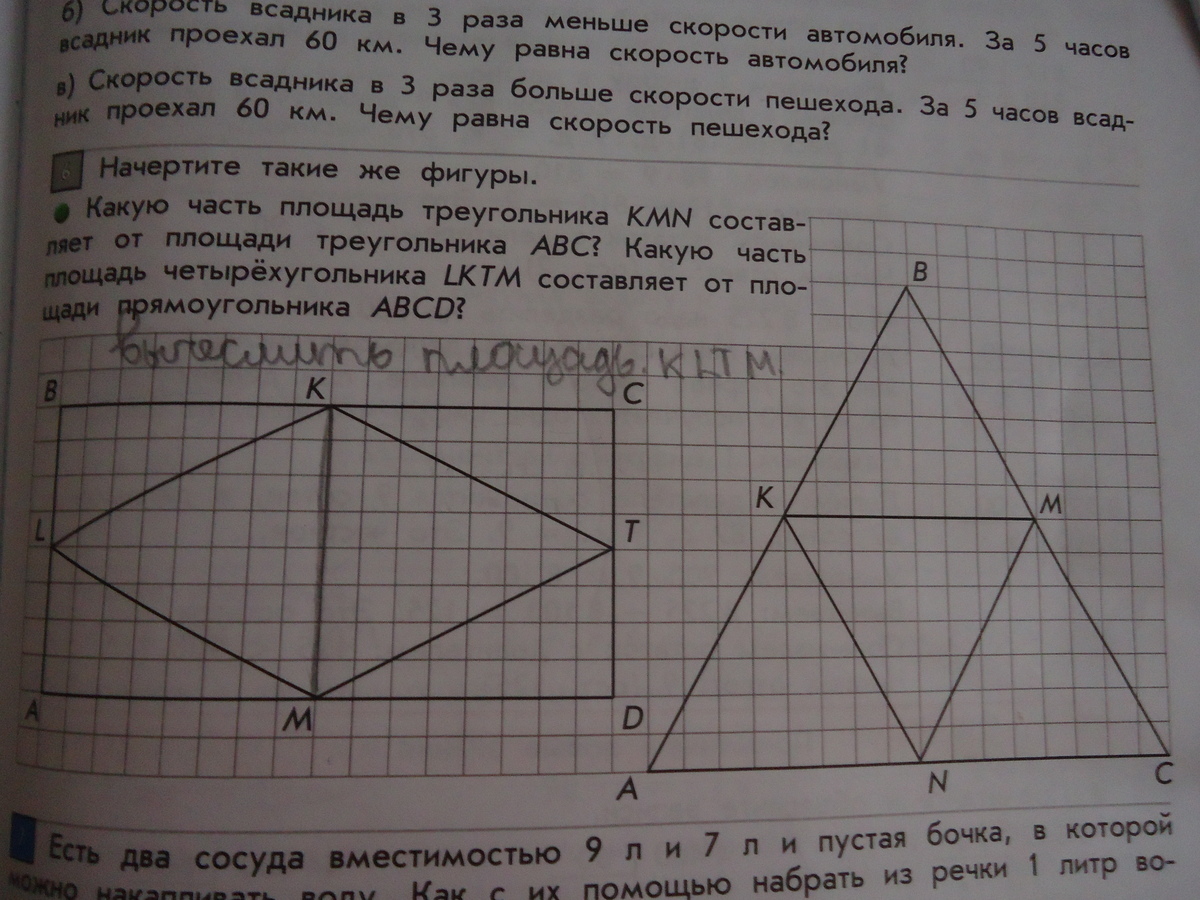
Какую часть площадь треугольника KMNКакую часть площадь треугольника KMN составляет от площади треугольника ABC? Какую часть площадь четырёхугольника LKTM cоставляет от площади прямоугольника АBCD??????????????
Приложения:
Ответы
Ответ дал:
0
Теорема.
Если в четырехугольнике противолежащие углы равны, такой четырехугольник – параллелограмм.
Доказательство.
Пусть дан четырехугольник ABCD. ∠ DAB = ∠ BCD и ∠ ABC = ∠ CDA.
Проведем диагональ DB. Сумма углов четырех угольника равна сумме углов треугольников ABD и BCD. Так как сумма углов в треугольнике равна 180 º,
∠ DAB + ∠ BCD + ∠ ABC + ∠ CDA.= 360 º. Так как противолежащие углы в четырехугольнике равны, то ∠ DAB + #8736 ABC = 180 º и ∠ BCD + ∠ CDA = 180 º.
Углы BCD и CDA являются внутренними односторонними для прямых AD и ВС и секущей DC, их сумма равна 180 º, поэтому из следствия к теореме о признаке параллельности прямых, прямые AD и ВС параллельны. Так же доказывается, что AB || DC. Таким образом, четырехугольник ABCD – параллелограмм по определению. Теорема доказана.
Если в четырехугольнике противолежащие углы равны, такой четырехугольник – параллелограмм.
Доказательство.
Пусть дан четырехугольник ABCD. ∠ DAB = ∠ BCD и ∠ ABC = ∠ CDA.
Проведем диагональ DB. Сумма углов четырех угольника равна сумме углов треугольников ABD и BCD. Так как сумма углов в треугольнике равна 180 º,
∠ DAB + ∠ BCD + ∠ ABC + ∠ CDA.= 360 º. Так как противолежащие углы в четырехугольнике равны, то ∠ DAB + #8736 ABC = 180 º и ∠ BCD + ∠ CDA = 180 º.
Углы BCD и CDA являются внутренними односторонними для прямых AD и ВС и секущей DC, их сумма равна 180 º, поэтому из следствия к теореме о признаке параллельности прямых, прямые AD и ВС параллельны. Так же доказывается, что AB || DC. Таким образом, четырехугольник ABCD – параллелограмм по определению. Теорема доказана.
Похожие вопросы
2 года назад
2 года назад
7 лет назад
10 лет назад
10 лет назад
10 лет назад