Геометрия 8 класс, теорему синусов-косинусов не проходили, квадратные уравнения не решали. Пифагора проходили. Даю 15 баллов за решение и объяснение. Это всё задание, никаких дополнительных вводных нет.


Найти значение синуса и косинуса наименьшего угла прямоугольного треугольника, если: а) с – а = 1 см, b = 50 см;

Ответ:

Синус и косинус наименьшего угла прямоугольного треугольника соответственно равны: sin∠B = 0,039; cos∠B = 0,999.

Объяснение:

Требуется найти значение синуса и косинуса наименьшего угла прямоугольного треугольника, если: с – а = 1 см, b = 50 см.

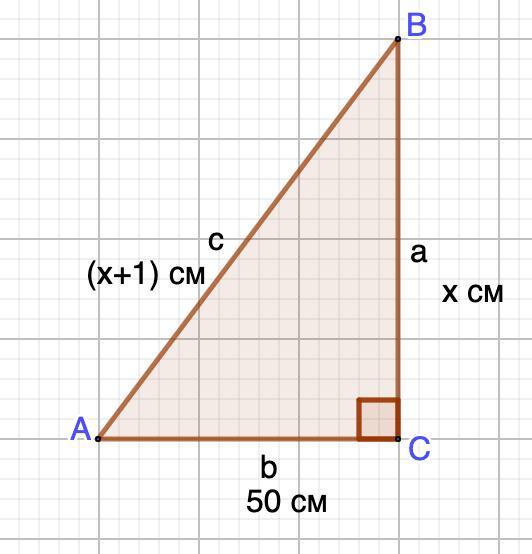
Дано: ΔАВС - прямоугольный.

с – а = 1 см, b = 50 см.

Найти: значение синуса и косинуса наименьшего угла.

Решение:

Для того, чтобы найти значение синуса и косинуса наименьшего угла, надо определить меньший угол.

Вспомним:

• Против меньшей стороны в треугольнике лежит меньший угол.

1. Пусть а = х см, тогда с = (х + 1) см

По теореме Пифагора:

с² = a² + b²

(x+1)² = x² + 50²

• Квадрат суммы двух чисел: (a + b)² = a² + 2ab + b²

Получим:

х² + 2х +1 = х² + 2500

х² + 2х - х² = 2500 - 1

2х = 2499   |:2

х = 1249,5

⇒ а = 1249,5 см;  с = 1249,5 + 1 = 1250,5 (см)

• Синус угла - отношение противолежащего катета к гипотенузе.
• Косинус угла - отношение прилежащего катета к гипотенузе.

b - меньшая сторона. Значит будем искать значение синуса и косинуса угла В.

Синус и косинус наименьшего угла прямоугольного треугольника соответственно равны: sin∠B = 0,039; cos∠B = 0,999.