14.6. 1) f(x) = -2x² + 2x - 4; помогите пожалуйста нужно сделать как на фото но бес слов ​

Ответ:

График квадратичной функции

f(x) = -2x² + 2x -4

построен.

Объяснение:

Построить график квадратичной функции

f(x) = -2x² + 2x -4

Дан график квадратичной функции вида: y = ах² + bx +c.

f(x) = -2x² + 2x - 4

- парабола, ветви вниз (а < 0)

1. Найдем координаты вершины:

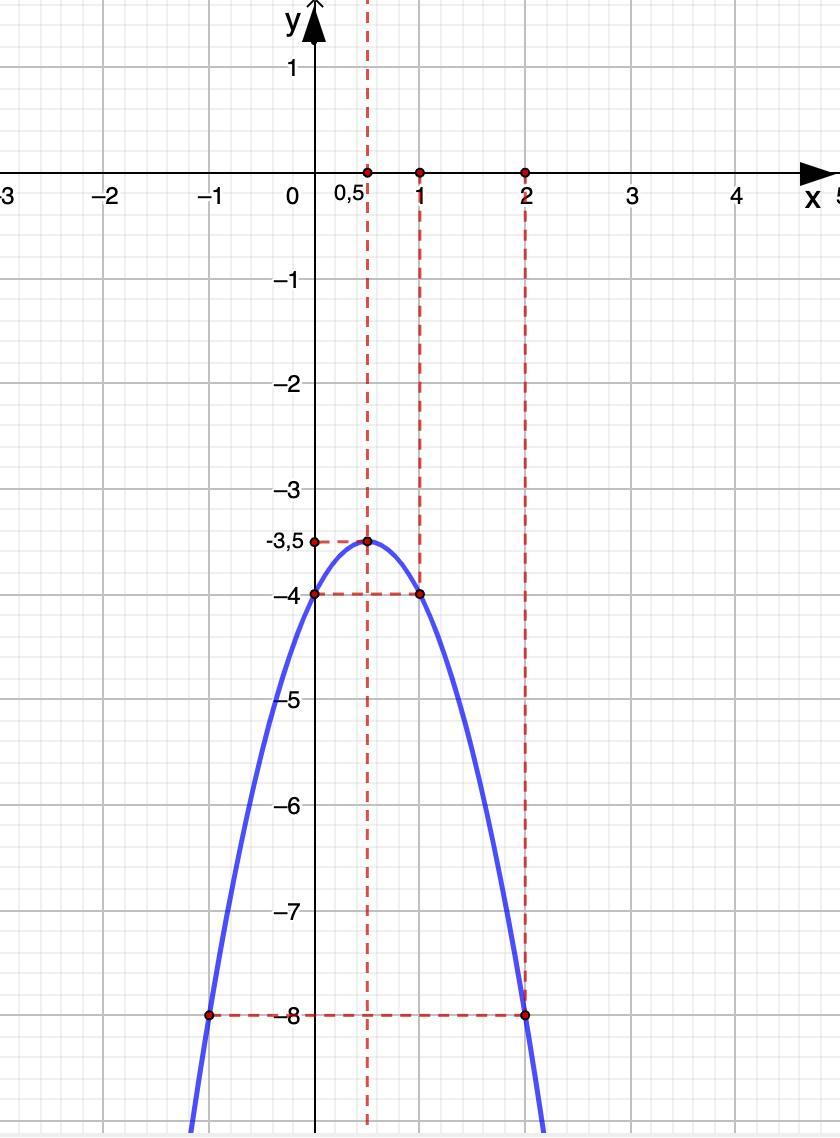
Координаты вершины (0,5; -3,5)

x = 0,5 - ось симметрии.

2. Найдем нули функции, другими словами, точки пересечения с осью 0х.

Решим уравнение

-2х² + 2х - 4 = 0     |:(-2)

x² - x + 2 = 0

D = 1 - 4 · 2 = -7

D < 0, корней нет.

Значит, ось 0х не пересекает.

3. Дополнительные точки:

х = 1;   у=-4;

х = 2;   у = -8.

Остальные точки построим симметрично прямой х = 0,5.

Соединим точки и построим график.