294. Внутри угла, равного 60°, дана точка, расстояния от которой
до сторон угла равны 2 см и 5 см. Найдите расстояние от этой
точки до вершины угла.

Если задача дана раньше синусов/косинусов, то надо разобрать треугольник с углами 30°, 60°, 90°.

Пусть гипотенуза - с, катет против угла 30° - a.

Катет против угла 30° равен половине гипотенузы, тогда c=2a.

По теореме Пифагора катет b =√(с^2-a^2) =√(4a^2-a^2) =a√3

a : b : c =  1 : √3 : 2

Стороны треугольника с углами 30°, 60°, 90° относятся как 1 : √3 : 2

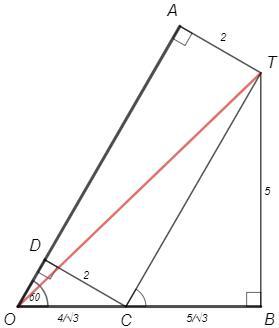
TA=2, TB=5

Проведем TC||AO, CD=TA=2 (расстояние между параллельными постоянно)

△COD с углами 30°, 60°, 90° => OC =DC 2/√3 =4√3

∠TCB=∠AOB=60° (накрест лежащие)

△TCB с углами 30°, 60°, 90° => CB =TB/√3 =5/√3

OB= 4√3 +5/√3 =9/√3 =3√3

△OTB, т Пифагора: TO=√(OB^2+TB^2) =√(27+25) =2√13 (см)

Внутри угла, равного 60°, дана точка, расстояния от которой

до сторон угла равны 2 см и 5 см. Найдите расстояние от этой

точки до вершины угла.

1) Пусть КН ⊥АВ и КС⊥ВС , тогда НК и КС -расстояния до сторон угла  ∠СВН . Пусть  НК=5 см и КС=2см.

2) Продолжим КС до пересечения с АВ .

ΔАВС-прямоугольный , ∠ВАС=90°-60°=30° ⇒ АВ=2ВС , по свойству угла в 30°.

3) ΔАНК-прямоугольный , по свойству угла в 30°, АК=5*2=10(см).

По т Пифагора для ΔАВС :АВ²=ВС²+АС²

(2ВС)²=ВС²+(10+2)² ⇒ ВС=4√3 см .

4) ΔВСК -прямоугольный .По т Пифагора АК²=ВС²+КС²,

АК²=(4√3)²+2² , АК²=48+4 , АК=√52=2√13(см)