СРОЧНО!!ДАМ 25 БАЛЛОВ!!!
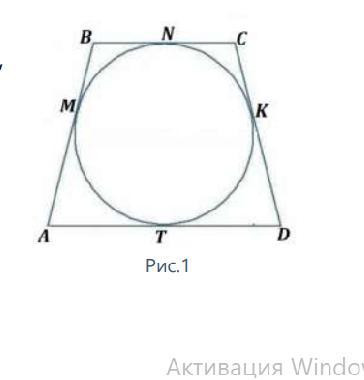
На рисунке 1 изображена

равнобедренная трапеция и окружность,

которая касается сторон трапеции в

точках М N K T. ∠A = 67°. Найдите

градусные меры дуг MN NK KT MT

Ответ:

MN = 67°;  NK = 67°;   KT = 113°;    MT = 113°.

Объяснение:

В равнобедренной трапеции

∠D = ∠A = 67°    и    ∠В = ∠С = 180° - 67° = 113°

Пусть О - центр окружности

Опустим перпендикуляры ОТ, ОМ, ОN. ОК.

Тогда

1) в четырёхугольнике АМОТ ∠М = ∠Т = 90° и

центральный угол ∠МОТ = 180° - 67° = 113°

Следовательно, градусная мера дуги МТ равна 113°.

2) в четырёхугольнике BNOM ∠М = ∠N = 90° и

центральный угол ∠МОN = 180° - 113° = 67°

Следовательно, градусная мера дуги МN равна 67°.

В силу симметрии трапеции относительно вертикальной оси, проходящей через центр окружности, можно утверждать, что

градусная мера дуги NK равна градусной мере дуги МN и равна 67°

и

градусная мера дуги КТ равна градусная мера дуги МТ  и равна 113°.