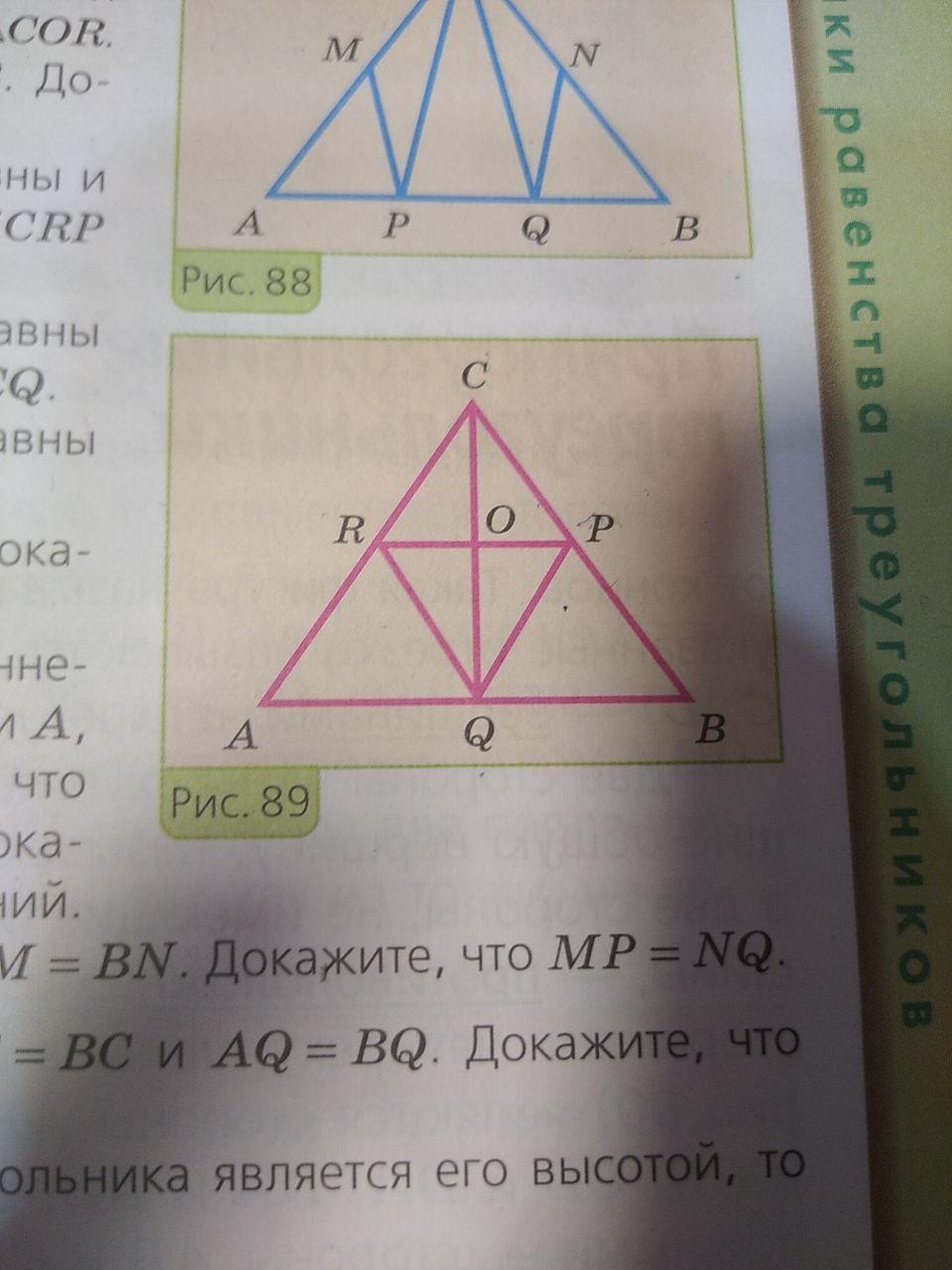
Отрезки PQ и RQ на рисунке 89 равны и ∠PQC = ∠RQC. Докажите, что ∠CPR = ∠CRP и CQ ⊥ PR.

Ответ:

треуг ORQ=OPQ по двум сторонам и углу между ними

(ОQ общая, PQ=RQ по условию, угол PQC=RQC по условию) → OR=OP,

треуг RPQ равнобедренный, RP основание, OQ - медиана, проведенная к основанию,

в равнобедренном треуг она одновременно является и высотой, значит,

CQ перпендикулярна RP