в равнобедренной трапеции угол при основании равен 45 градусов ,а основания равны 3 см и 7 см . найдите площадь трапеции
Ответы
Ответ дал:
1
Ответ:
10
Объяснение:
опустим перпендикуляры к нижнему основанию. так как угол А =45, а треугольник АВЕ равнобедренный ( тк угол В тоже равен 45), то ВЕ- высота=2 см.
площадь трапеции = 0,5*ВЕ*(ВС+АД)= 0,5*2*(3+7)=10
Приложения:
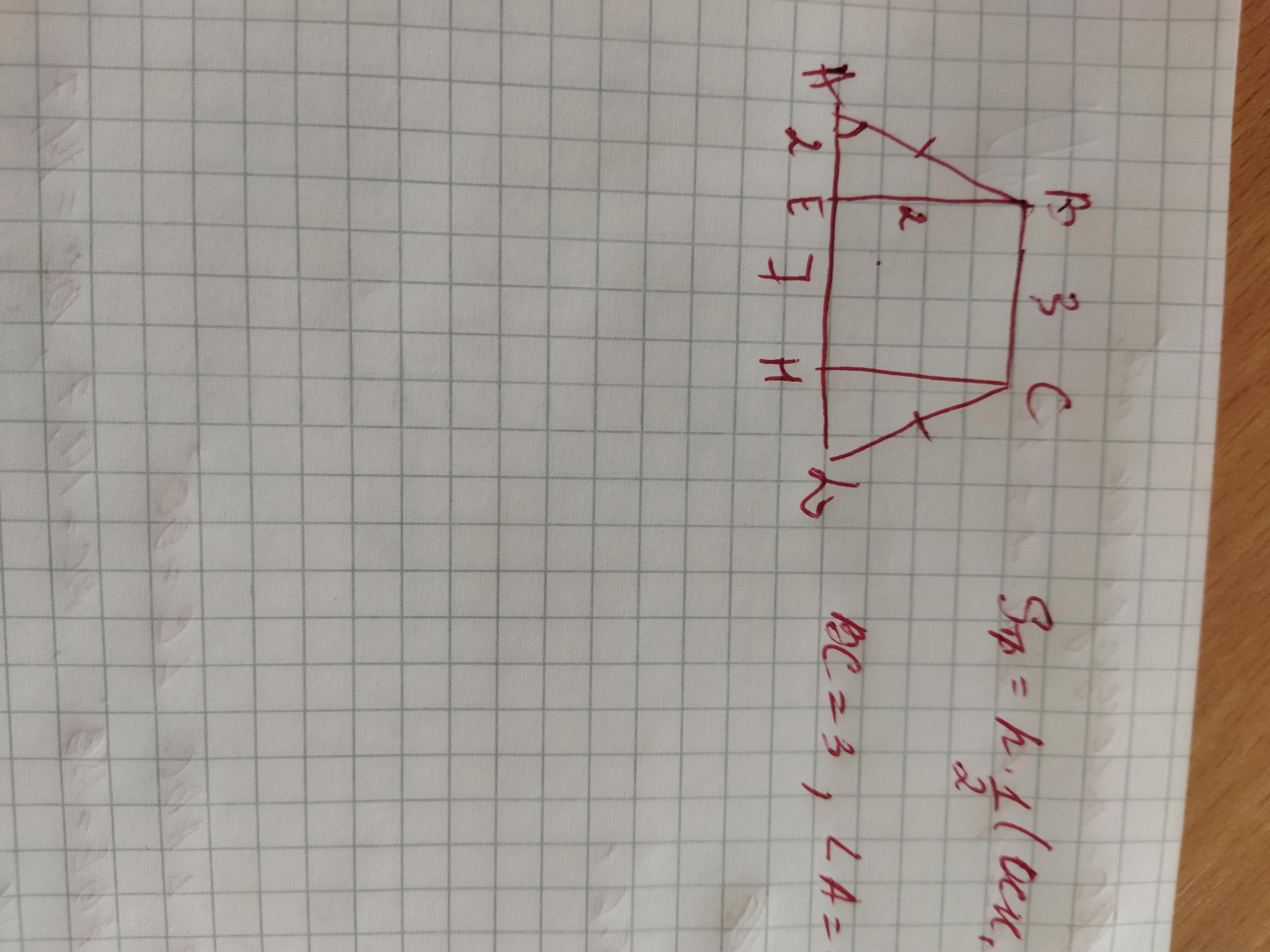
sovvalli2008:
спасибо!!
Ответ дал:
0
Ответ:
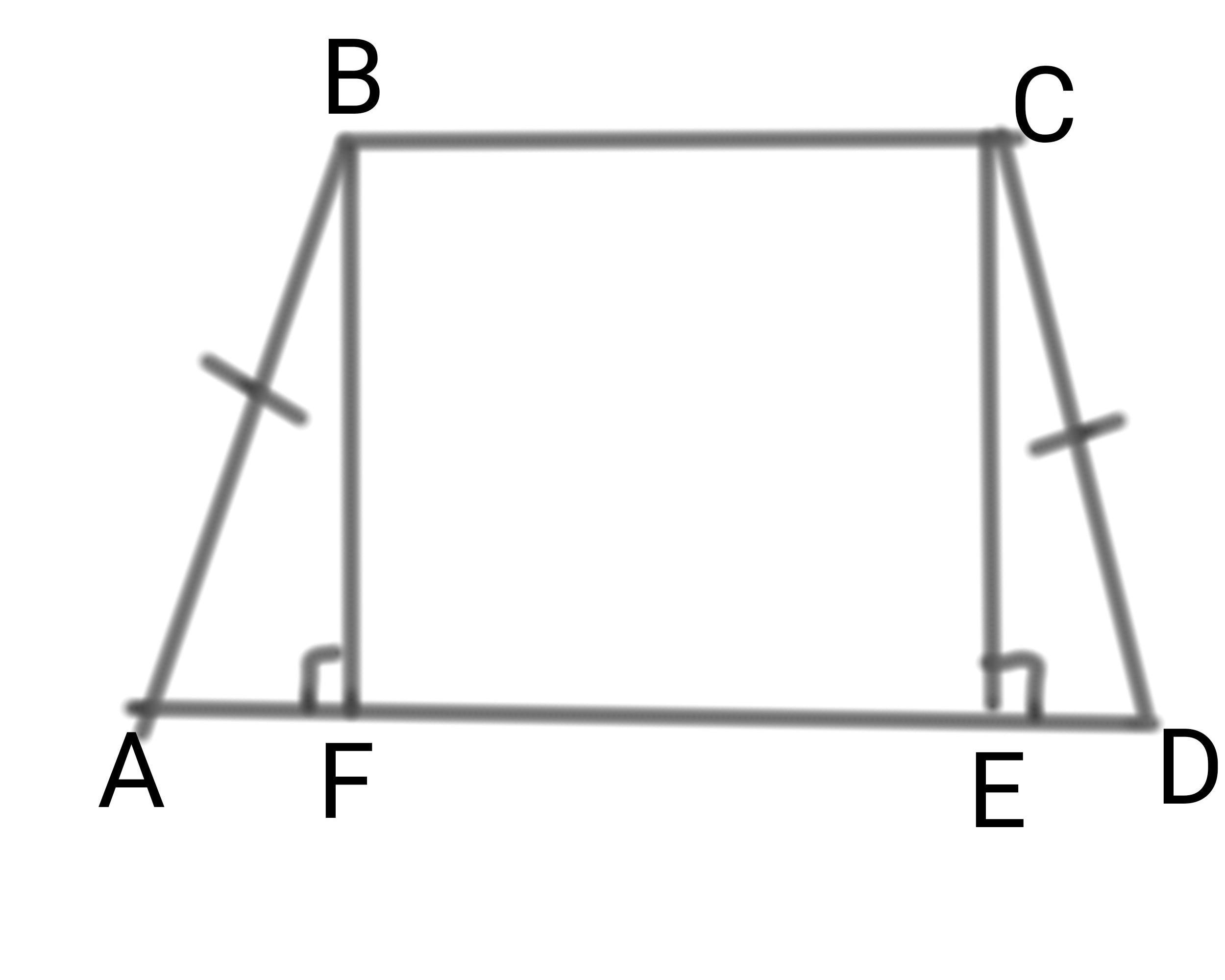
В трапеции ABCD угол A=45°.
AD=7, BC=3
Опустим высоты BF и CE, получится, что ΔABF – равнобедренный прямоугольный треугольник. Значит AF=BF.
BC=EF, потому что BCEF – прямоугольник.
EF=3
AF+ED+EF=AD
AF+ED=AD-EF
AF+ED=7-3
AF+ED=4
AF=ED=4:2=2
AF=BF=2
Формула площади трапеции:
где a, b – основания, h – высота.
S=10 см²
Приложения:
Похожие вопросы
1 год назад
1 год назад
2 года назад
2 года назад
8 лет назад