в прямоугольном треугольнике гипотенуза равна 65 см, а тангенс одного из углов 2/9. найдите катеты этого треугольника.

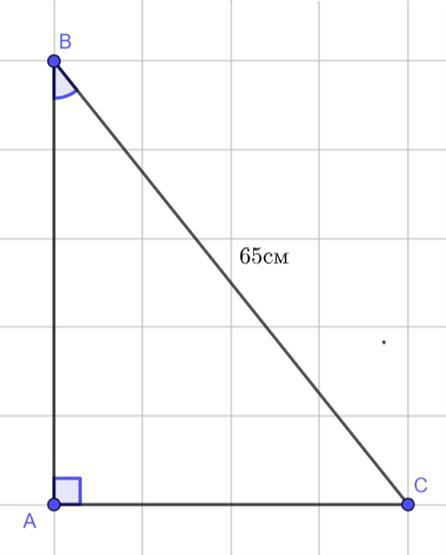
Дано:

∠A = 90°;

tg ∠B = ;

BC = 65 см.

Найти:

AB; AC.

                                        Решение:

Тангенс острого угла прямоугольного треугольника равен отношению противолежащего катета к прилежащему.

Это значит, что AC относится к AB как 2 : 9.

Обозначим коэффициент пропорциональности как x.

Тогда AC = 2x, AB = 9x.

По теореме Пифагора, сумма квадратов катетов равна квадрату гипотенузы:  

AC² + AB² = BC²;

(2x)² + (9x)² = 65²;

4x² + 81x² = 4225;

85x² = 4225;

x² = 4225 : 85;

x² ≈ 49,7;

x = ;

x ≈ 7,05.

AC = 2x = 2 ∙ 7,05 = 7,1 (см).

AB = 9x = 9 ∙ 7,05 = 63,45 (см).

Ответ: катеты треугольника равны 7,1 см и 63,45 см.