• Предмет: Геометрия
  • Автор: LolikValedolik
  • Вопрос задан 6 лет назад
< >

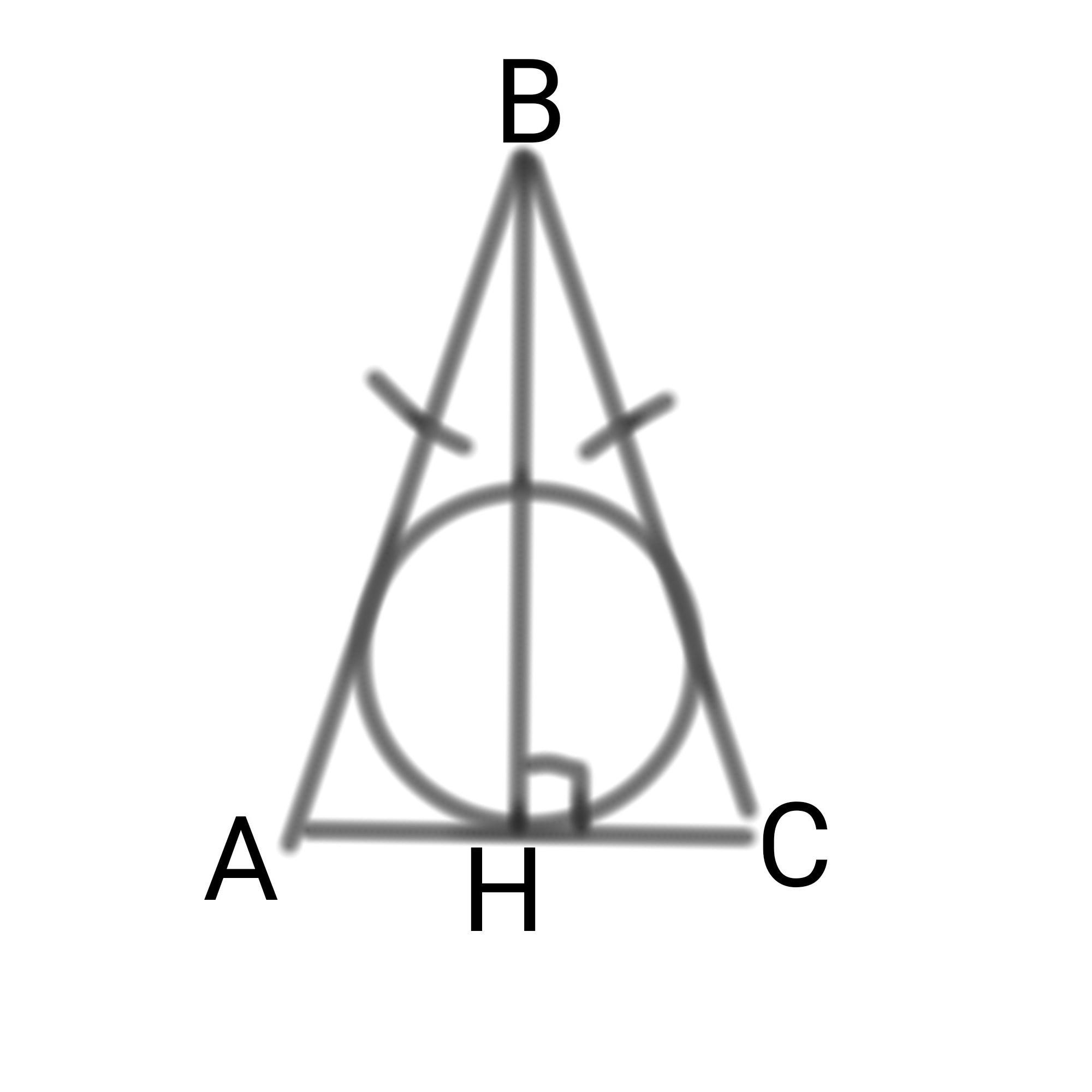
в равнобедренном треугольнике abc боковые стороны ab=bc=25 а высота bh 20 Найдите длину окружности вписанной в треугольник abc. Срочно!!! ​

Приложения:

Ответы

Ответ дал: bertramjeratire
1

Ответ:

AB=25

BC=25

BH=20

Высота BH является одновременно и медианой, и биссектрисой, потому что это равнобедренный треугольник.

Рассмотрим треугольник ΔABH, он прямоугольный.

По теореме Пифагора, квадрат гипотенузы равен сумме квадратов катетов.

AB²=AH²+BH²

AH²=AB²-BH²

AH = \sqrt{ {25}^{2} - {20}^{2} } \\ AH = \sqrt{625 - 400} \\ AH = \sqrt{225} \\ AH = 15

AH=CH, потому BH – медиана и делит сторону пополам.

AC=15+15=30

Радиус вписанной окружности вычисляется по формуле

r=\frac {2S} {P}

S – площадь треугольника, P – периметр треугольника.

Найдем площадь:

S = \frac{1}{2} \times a \times h

Важно учесть, что должна браться сторона, к которой опущена высота h. У нас известна высота BH к стороне AC.

S = \frac{1}{2} \times 30 \times 20 \\ S = 30 \times 10 \\ S = 300

P=AB+BC+AC

P=25+25+30=80

Теперь найдем радиус вписанной окружности:

r = \frac{2 \times 300}{80} = \frac{600}{80} = \frac{15}{2} = 7.5

Формула длины окружности:

L=2πr

L = 2\pi \times 7.5 = 15\pi

Длина вписанной окружности 15π

Приложения:
marshal500: Вы площадь делили на периметр, а надо на полупериметр.
bertramjeratire: Я удвоенную площадь делил на периметр, выше доказал, что нет разницы
marshal500: да уж... весьма вольное трактование формул... Вы все формулы переиначиваете?... зачем?... есть конкретное выражение - "Радиус окружности, вписанной в равнобедренный треугольник, равен отношению площади треугольника к его полупериметру." - это цитата... зачем её переиначивать?
bertramjeratire: Я не сам эту придумал формулу и не брал из воздуха, зачем исправлять то, что является истиной?
bertramjeratire: Есть цитата "Радиус окружности, вписанной в любой треугольник, равняется удвоенной площади треугольника, деленной на его периметр."
bertramjeratire: Если не лень, можете в поисковике пробить
marshal500: по Вашему я из воздуха эту цитату привел?
bertramjeratire: Я не говорил, что это ошибка, я спросил зачем мне исправлять то, что является правильным
marshal500: согласен. правильно. я просто по инерции не увидел двойку перед площадью. именно по этому и разногласие. исправлять не надо.
bertramjeratire: Ну ладно, бывает
Похожие вопросы
Английский язык
1 год назад
Помогите пожалуйста!!!
Русский язык
1 год назад
план соченения мой друг
Английский язык
2 года назад
Грамотно составить предложения на английском языке : 1 Япротив хакеров так как восновном это больные люди. 2 У них часто возникают проблемы со зрением. 3 Они наносят вред корпорациям взламывая их . 4
Русский язык
2 года назад
Морфологический разбор слова  старое
Математика
8 лет назад
Среди натуральных чисел 1, 2, ..., А (от одного до А) ровно восемь чисел делятся на 6 и ровно шесть чисел делятся на 7. Найдите число А.
Математика
8 лет назад
Среднее арифметическое трёх чисел равно 6целых 17/24.Первое число в 2целых 1/45 меньше второго,а второе на 1целую 5/24 меньше третьего.Найдите эти числа.
Химия
9 лет назад
2KOH + ZnCl2 = 2KCl + Zn(OH)2 Скажите пожалуйста какого цвета осадок) очень надо)
Математика
9 лет назад
В прямоугольнике диагональ равна 10 см и составляет с одной из сторон угол 42 градуса . Найдите площадь прямоугольника.