Точка М принадлежит одной из граней двугранного угла и удалена от
его ребра на 4 см. Найдите расстояние от точки M до другой грани угла, если величина этого угла равна 45°.​

Ответ:

2√2 см

Объяснение:

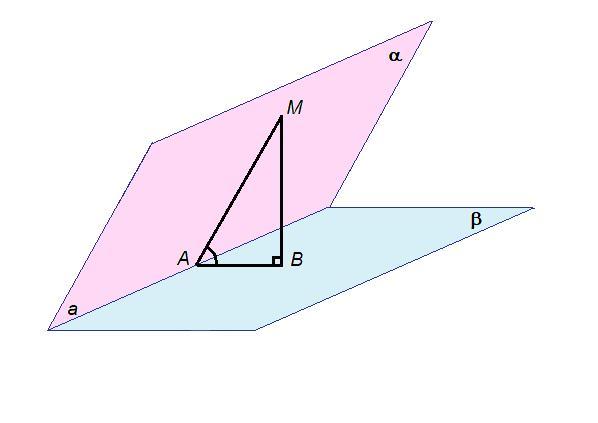
Двугранный угол образован плоскостями α и β. Прямая а - линия пересечения плоскостей.

M∈α.

Проведем МА ⊥ а. МА = 4 см - расстояние от точки М до ребра двугранного угла.

Проведем МВ ⊥ β. МВ - искомое расстояние.

МА ⊥ а, АВ - проекция МА на плоскость β, значит МВ ⊥ а по теореме, обратной теореме о трех перпендикулярах. Тогда

∠МАВ = 45° - линейный угол двугранного угла.

ΔМАВ:  ∠МВА = 90°, ∠МАВ = 45°

   см