НОЧНО1Й АКТИВ. 60 БАЛЛОВ!​

Ответ:

Есть правило:

Медиана, проведенная к гипотенузе, равна половине гипотенузы прямоугольного треугольника.

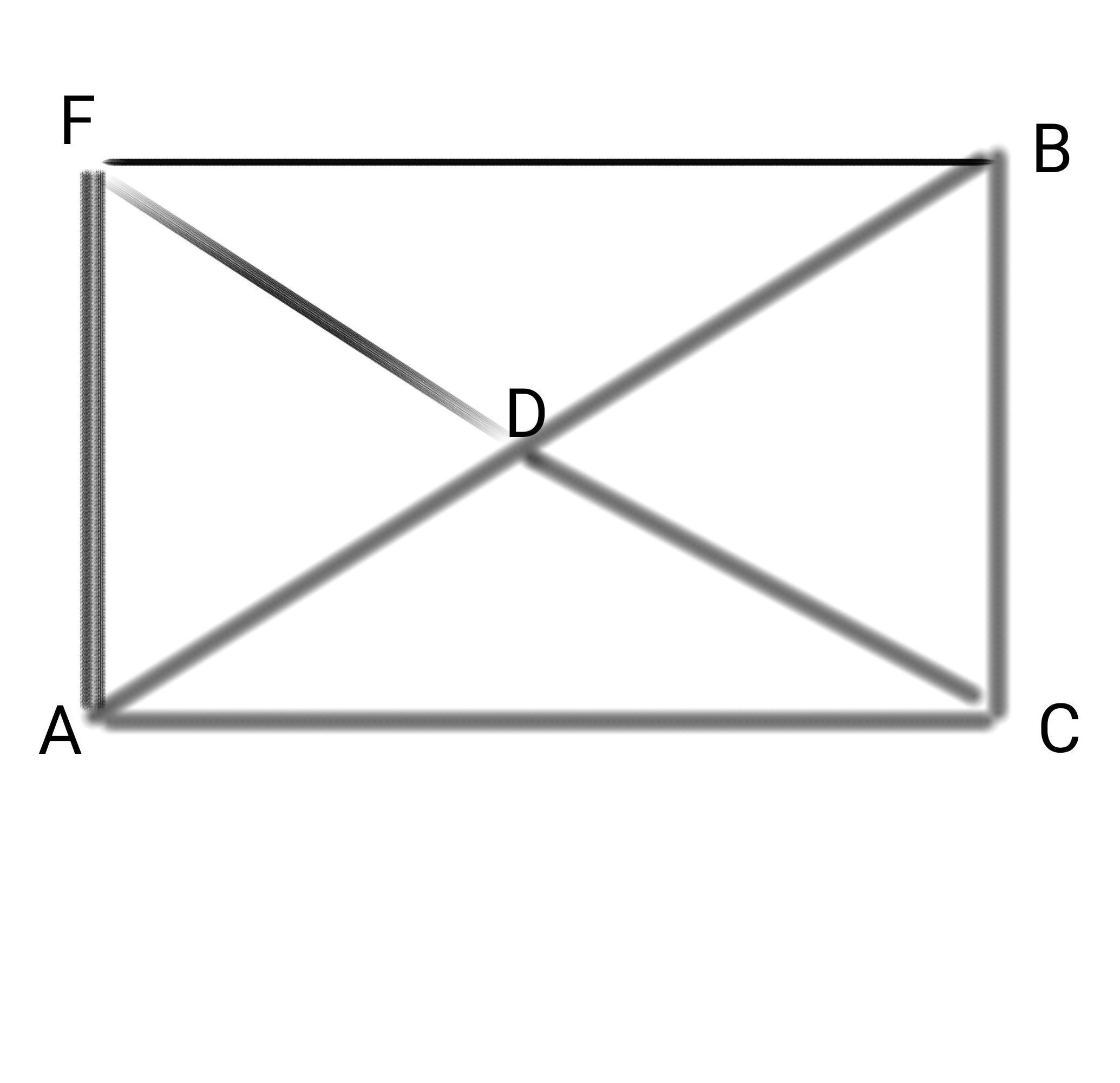
А если углубиться, то надо достроить прямоугольный треугольник ABC до прямоугольника ACBF.

Получается, что AB и CF – диагонали, а диагонали прямоугольника равны и делятся точкой пересечения D пополам.

Значит CD=CF/2 и так как CF=AB,

CD=AB/2, то есть половина гипотенузы.

P.S углы прямоугольника естественно прямые, поэтому, если медиана CD равна половине AB, то угол ACD=90°

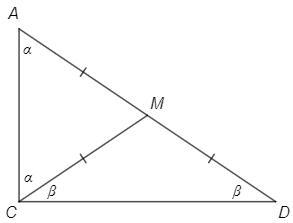
M - середина AD, CM - медиана

CM=1/2 AD => CM=AM=DM

△AMC - равнобедренный (AM=CM) => ∠A=∠ACM =a

△CMD - равнобедренный (CM=DM) => ∠MCD=∠D =b

∠ACD =∠ACM+∠MCD =a+b

△ABC: ∠A+∠ACD+∠D=180° => a+a+b+b=180° => a+b=90° =∠ACD