помогите пожалуйста решить задачу по геометрии 8 класс ​

Ответ:

BH = 20 ед.

Объяснение:

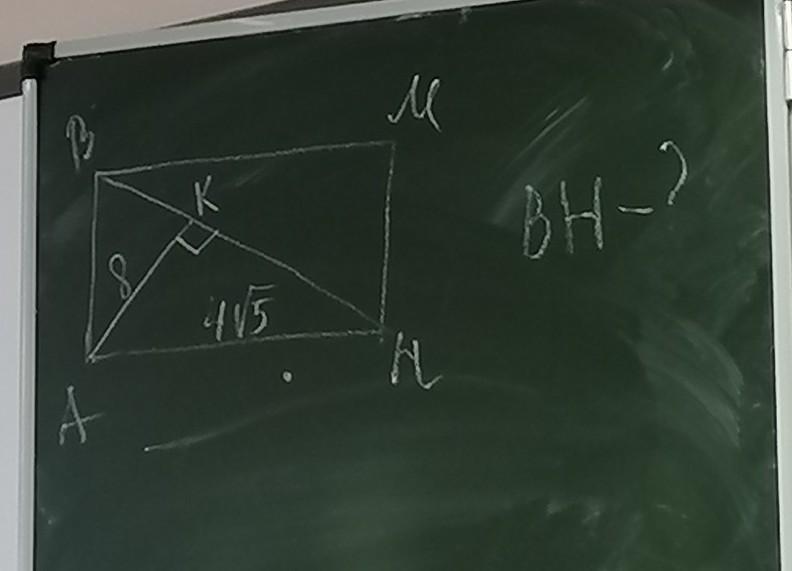
Рассмотрим рисунок. На рисунке задан треугольник  ΔАВН прямоугольный. В нем проведена высота АК.

АК = 8 ед., АН = 4√5 ед.

Рассмотрим Δ АКН - прямоугольный.

По теореме Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Дальше воспользуемся свойством высоты прямоугольного треугольника: высота прямоугольного треугольника , проведенная к гипотенузе, есть среднее геометрическое между отрезками гипотенузы, на которые она делится основанием высоты.

Тогда