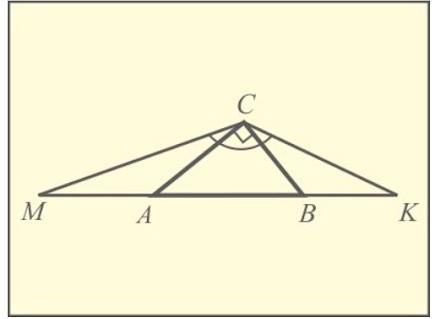
На прямой проходящей через гипотенузу АВ прямоугольного треугольника АВС взяты точки М и К, так, что АМ = АС и ВК = ВС. Найдите угол МСК.​

AM=AC, MAC - равнобедренный

Углы при основании равнобедренного треугольника равны.

∠M=∠MCA

Внешний угол треугольника MAC равен сумме внутренних, не смежных с ним.

∠CAB =∠M+∠MCA => ∠CAB=2∠M

Аналогично из треугольника KBC: ∠CBA=2∠K

Сумма острых углов прямоугольного треугольника 90°.

∠CAB+∠CBA=90° => 2∠M+2∠K=90° => ∠M+∠K=45°

Из треугольника MCK: ∠MCK=180°-∠M-∠K =180°-45° =135°