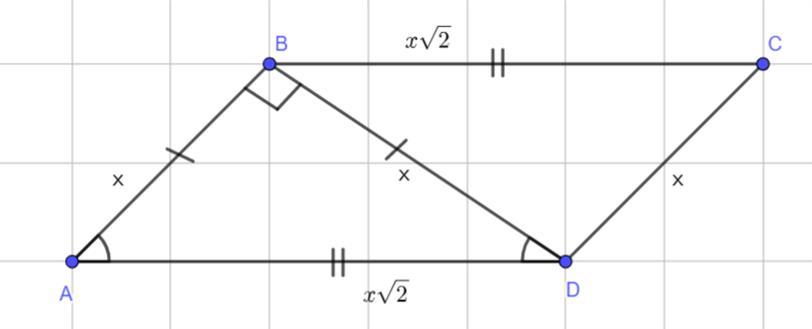
тупий кут паралелограма дорівнює 135°. Діагональ паралелограма ділить його у відношенні 1:2. знайдіть цю діагональ, якщо периметр паралелограма дорівнює 60см

Ответы

Ответ дал: polinabognibova

Відповідь: 30(√2 - 1) см.

_________________________________________

Дано:

ABCD — паралелограм;

∠ABC = 135°;

∠CBD : ∠DBA = 1 : 2;

$P_{ABCD}$ = 60см.

Знайти:

BD.

Розв'язання:

Кути, на які діагональ BD ділить ∠ABC, відносяться як 1 : 2. Якщо коефіцієнт пропорційності дорівнює k, то ∠CBD = k, ∠DBA = 2k. Так як ∠ABC = 135°, маємо рівняння:

k + 2k = 135

3k = 135

k = 135 : 3

k = 45

∠DBA = 2 · 45 = 90.

Значить, ΔABD є прямокутним.

Сума кутів паралелограма, що лежать на одній стороні, складає 180°, тому: ∠BAD = 180 - 135 = 45°.

Коли в прямокутного трикутника один з гострих кутів дорівнює 45°, цей трикутник є рівнобедреним.

Тому AB = BD.

Позначимо їх за х. Тоді за теоремою Піфагора:

AD² = x² + x² = 2x²

AD = $\sqrt{2x^2}= x\sqrt{2}$ (см).

У паралелограма протилежні сторони рівні. Зважаючи на це, можемо записати формулу його периметру:

$P_{ABCD}$ = 2(AD + AB) = 2(х√2 + x)

Нам відомо, що периметр дорівнює 60 см, тож:

2(х√2 + x) = 60

х√2 + x = 60 : 2

х√2 + x = 30

Винесемо спільний множник за дужки:

х(√2 + 1) = 30

Виразимо х:

$\displaystyle x = \frac{30}{\sqrt{2} +1}$

Позбудемося ірраціональності в знаменику дробу. Можна доповнити його до формули (a + b)(a - b) = a² - b². Для цього слід і чисельник, і знаменик помножити на вираз (√2 - 1):

$\displaystyle x = \frac{30}{\sqrt{2} +1 } =\frac{30(\sqrt{2}-1) }{(\sqrt{2}+1)(\sqrt{2}-1) } = \frac{30(\sqrt{2}-1) }{(\sqrt{2})^2 - 1^2 } = \frac{30(\sqrt{2}-1)}{2-1}= 30(\sqrt{2}-1)$ .