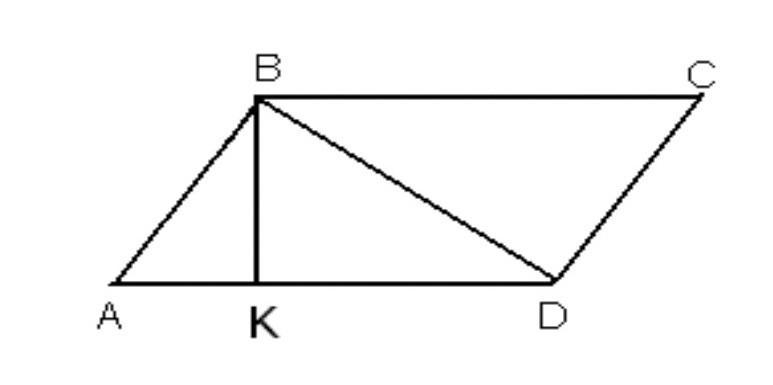
В параллелограмме ABCD угол ABK = угол KBD, AB = 6 × AK и периметр треугольника ABD = 42. Найдите BC. ​

Ответ:  ВС=6 .

АВСД - паралл-м , ∠АВК=∠КВД  ⇒  ВК - биссектриса , АВ=ВД  ,  АВ=6*АК ,  Р(АВД)=42 .

Обозначим АК=х   ⇒  АВ=6х  ,  

Так как ВК - биссектриса, то по свойству биссектрисы можно записать отношение  АК : АВ=КД : ВД  , то есть

 х : 6х=КД : ВД  ,   КД : ВД = 1 : 6 .

Обозначим  КД=у  , тогда  ВД=6у .

Периметр Р(АВД)=АВ+ВД+АД=АВ+ВД+(АК+КД)=6х+6у+(х+у)=7(х+у)  ,  7(х+у)=42  ,

х+у=6  ⇒   АД=6

Но в параллелограмме противоположные стороны равны, поэтому  АД=ВС=х+у=6 .