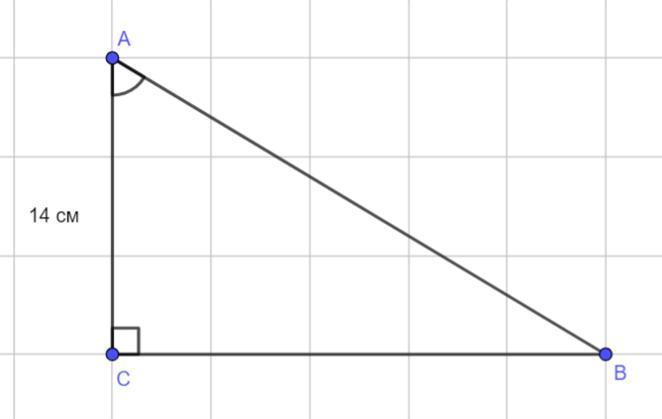
У трикутнику ABC (C=90°) АС=14 см, sinA= 24/25 Знайдіть
периметр трикутника.
Помогите пж это кр с геометрии:/

Відповідь: 112 см.

_______________________________________

Дано:

∠C = 90°,

АС = 14 см,

.

__________

— ?

                                           Розв'язання:

• Спосіб № 1:

Синус гострого кута прямокутного трикутника дорівнює відношенню протилежного катета до гіпотенузи:

Значить, CB відноситься до АВ як 24 : 25. Нехай коефіцієнт пропорційності х, тоді:

СВ = 24х, АВ = 25х.

За теоремою Піфагора, сума квадратів катетів прямокутного трикутника дорівнює квадрату гіпотенузи:

AC² + СВ² = АВ²

Підставимо у формулу отримані значення:

14² + (24х)² = (25х)²

196 + 576х² = 625х²

196 = 625х² - 576х²

196 = 49х²

х² = 196 : 49

х² = 4

х = √4

х = 2

СВ = 24 · 2 = 48,

АВ = 25 · 2 = 50.

Знайдемо периметр трикутника (це сума всіх його сторін):

(см).

• Спосіб №2:

Використаємо основну тригонометричну тотожність:

(оскільки ∠А гострий, значення його косинуса має бути додатнє, тож перед коренем ставимо знак "плюс").

Косинус гострого кута прямокутного трикутника дорівнює відношенню прилеглого катета до гіпотенузи:

Звідси,

Синус гострого кута прямокутного трикутника дорівнює відношенню протилежного катета до гіпотенузи:

Звідси, (см).

(см).