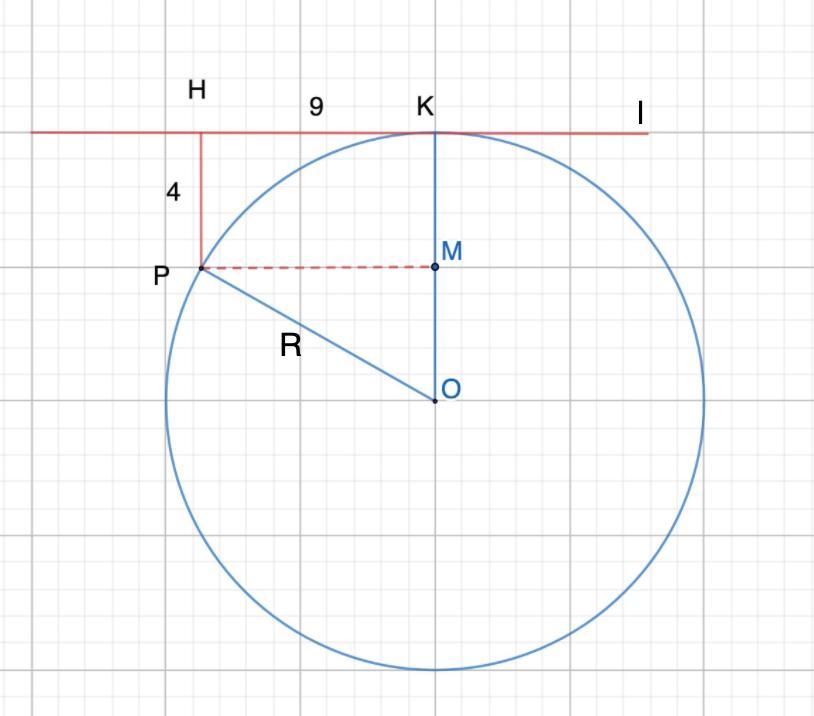
Прямая l касается окружности w в точке K. На окружности выбрана точка Р; Н- проекция Р на прямую l (отрезок РН не имеет общих точек с w кроме точки Р). Найдите радиус w, если РН=4, НК=9
Срочно!!!!! помогите пожалуйста ​

Ответ:

Радиус окружности ω равен  ед.

Пошаговое объяснение:

Требуется найти радиус окружности ω.

Дано: ω(О, R)

l - касательная;

К - точка касания;

Н- проекция Р на прямую l;

РН = 4, НК = 9.

Найти: R

Решение:

• Проекция точки на прямую – это основание перпендикуляра, опущенного из этой точки на заданную прямую.

⇒ РН ⊥ НК

• Радиус, проведенный в точку касания перпендикулярен касательной.

⇒ ОК ⊥ НК

Проведем РМ ⊥ ОК.

Получим РНКМ - прямоугольник.

• Противоположные стороны прямоугольника равны.

⇒ НК = РМ = 9; РН = МК = 4.

Рассмотрим ΔРМО - прямоугольный.

ОР = ОК = R.

Пусть ОР = х, тогда МО = (х - 4)

По теореме Пифагора:

ОР² = МО² + РМ²

х² = (х - 4)² + 9²

х² = х² - 8х + 16 + 81

8х = 97   |:8

Радиус окружности ω равен  ед.