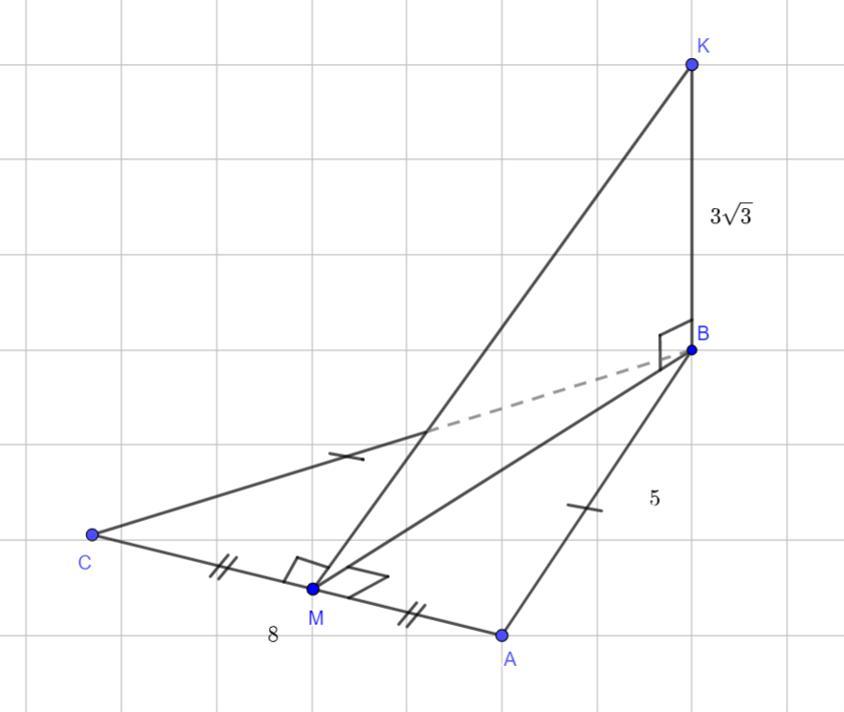
Из вершины В равнобедренного треугольника АВС (АВ=ВС) к плоскости треугольника проведен перпендикуляр ВК=3√3 см.

Найти расстояние от точки К до стороны АС, если АС=8 см, АВ=5 см.

Дано:

АВ=ВС;

ВК ⊥ (ABC);

ВК=3√3 см;

АС=8 см;

АВ=5 см;

_______

KM — ?

                                            Решение:

Соединим точки B и М.

Когда прямая перпендикулярна плоскости, она перпендикулярна всем прямым, принадлежащим этой плоскости. Поэтому ВК ⊥ BM.

KM — наклонная к плоскости (ABC), BM — проекция наклонной.

Расстоянием от точки до прямой является перпендикуляр, проведенный из этой точки к прямой. Поэтому КМ ⊥ AC.

По теореме о 3 перпендикулярах, если прямая, проходящая через основание наклонной, перпендикулярна наклонной, то она перпендикулярна и ее проекции.

Значит, AC ⊥ BM. Тогда BM — высота равнобедренного треугольника, проведенная к основанию. Такая высота является также медианой.

Поэтому AM = AC : 2 = 8 : 2 = 4 (см).

Рассмотрим прямоугольный ΔAMB. По теореме Пифагора:

AB² = BM² + AM² .

BM² = AB² -  AM² = 5² - 4² = 25 - 16 = 9.

BM = √9 = 3 (см).

Теперь рассмотрим прямоугольный ΔKBM. По теореме Пифагора:

KM² = KB² + BM² = (3√3)² + 3² = 27 + 9 = 36.

KM = √36 = 6 (cм) — расстояние от точки К до стороны AC.

Ответ: 6 см.