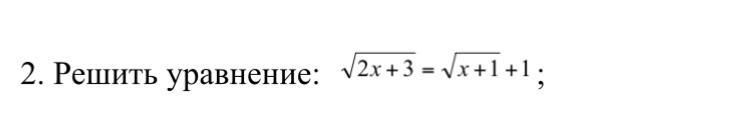Предмет: Математика
Автор: shhhhm1
Вопрос задан 6 лет назад

Срочно,пожалуйста!!!!

Приложения:

Ответы

Ответ дал: Amelie13

Ответ: -1; 3

Пошаговое объяснение: Обе части уравнения гарантированно больше нуля, следовательно, можно возвести в квадрат: 2x + 3 = x + 1 + 1 + 2*sqrt(x + 1).
2x - x + 3 - 2 = 2sqrt(x + 1)
x + 1 = 2sqrt(x + 1)
(x + 1) /2 = sqrt(x + 1)
Преобразуем в систему:
(x + 1) /2 >= 0 и 4x + 4 = x^2 + 2x + 1
x >= -1 и x^2 - 2x - 3 = 0
=> x = -1 или x = 3

shhhhm1: Сможешь решить другой пример ?

Ответ дал: atsuri

Ответ:

x₁ = - 1; x₂ = 3

Пошаговое объяснение:

$\sqrt{2x+3}=\sqrt{x+1}+1$

возведём обе части уравнения в квадрат:

$(\sqrt{2x+3})^2=(\sqrt{x+1}+1)^2$

правая часть по формуле $(a+b)^2=a^2+2ab+b^2$ :

$2x+3=x+1+2\sqrt{x+1}+1$

перенесём $2\sqrt{x+1}$ в левую часть уравнения, а остальные слагаемые в правую. при переносе через знак равенства, каждый из слагаемых меняет знак на противоположный.

$-2\sqrt{x+1}=x+2-2x-3\\\\-2\sqrt{x+1}=-x-1$

возведём обе части уравнения в квадрат:

$(-2\sqrt{x+1})^2=(-x-1)^2$

правая часть по формуле $(a-b)^2=a^2-2ab+b^2$ :

$4(x+1)=x^2+2x+1\\\\4x+4=x^2+2x+1\\\\4x+4-x^2-2x-1=0\\\\-x^2+2x+3=0\;\;|\cdot(-1)\\\\x^2-2x-3=0\\\\D=(-2)^2+4\cdot3=4+12=16\\\\x_{1,2}=\dfrac{2\pm\sqrt{16}}{2}=\dfrac{2\pm4}{2}\\\\x_1=\dfrac{2-4}{2}=\dfrac{-2}{2}=-1\\\\x_2=\dfrac{2+4}{2}=\dfrac{6}{2}=3$