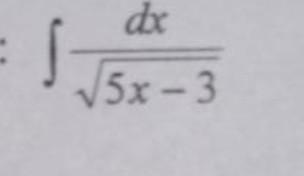Найти неопределенный интеграл

Приложения:

Ответы

Ответ дал: Аноним

(1/5)∫d(5x-3)/(√(5x-3))=(2√(5x-3)/5)+c

Ответ дал: mathkot

Ответ:

$\boxed{\displaystyle \int {\dfrac{dx}{\sqrt{5x - 3} } } \, = \dfrac{2\sqrt{5x - 3} }{5} + C}$

Примечание:

$\boxed{\displaystyle \int {x^{n}} \, dx = \dfrac{x^{n + 1}}{n + 1} + C, n \neq 1, x > 0}$ - по таблице первообразных

Объяснение:

$\displaystyle \int {\dfrac{dx}{\sqrt{5x - 3} } } \, = \frac{1}{5} \int {\dfrac{d(5x - 3)}{\sqrt{5x - 3} } } \, = \frac{1}{5} \int (\sqrt{5x - 3})^{-1} \,d(5x - 3) =$

$= \displaystyle \frac{1}{5} \int {(5x - 3)^{-0,5}} \,d(5x - 3) = \frac{1}{5} \cdot {(5x - 3)^{-0,5 + 1} \cdot \dfrac{1}{-0,5 + 1} + C =$

$= \displaystyle \frac{1}{5 \cdot 0,5} (5x - 3)^{0,5} + C = \dfrac{2\sqrt{5x - 3} }{5} + C$

Похожие вопросы

Математика

1 год назад

Моторная лодка доплывает от пристани А до пристани Б, через 6 часов. Расстояние между пристанями равно 12 км. За какое время плот, отправленный от пристани Б дойдёт до пристани А, если собственная

Русский язык

1 год назад

Найдите в тексте глаголы неопределённой формы и запишите их с вопросом что делать? или что сделать? Выделите в них суффиксы. Вы захотите сказать, что такого не может произойти. Но имеются места на

Алгебра

2 года назад

Представьте в виде произведения : (5х - 2у)в квадрате - 9у в квадрате =

Математика

2 года назад

В день рождения к Наташе должны были прийти либо 3, либо 4 гостя. Для гостей был приготовлен рулет, который хозяйка хочет разрезать так, чтобы его можно было раздать поровну. При этом желательно,

Математика

8 лет назад

В парке 150 деревьев. Берёзы составляют 2/5 всех деревьев. Сколько берёз в парке?

Обществознание

8 лет назад

обьясните смысл понятий : "гражданин", "гражданство".

Математика

9 лет назад

расставь в данном выражении скобки так чтобы значение выражения равнялось 4+5×7-2

История

9 лет назад

Зачем нужны победы Риму?

Найти неопределенный интеграл​

Ответы

Найти неопределенный интеграл