помогите доказать. рисунок обязательно​

Ответ:

R ⊥ BD = 0

Объяснение:

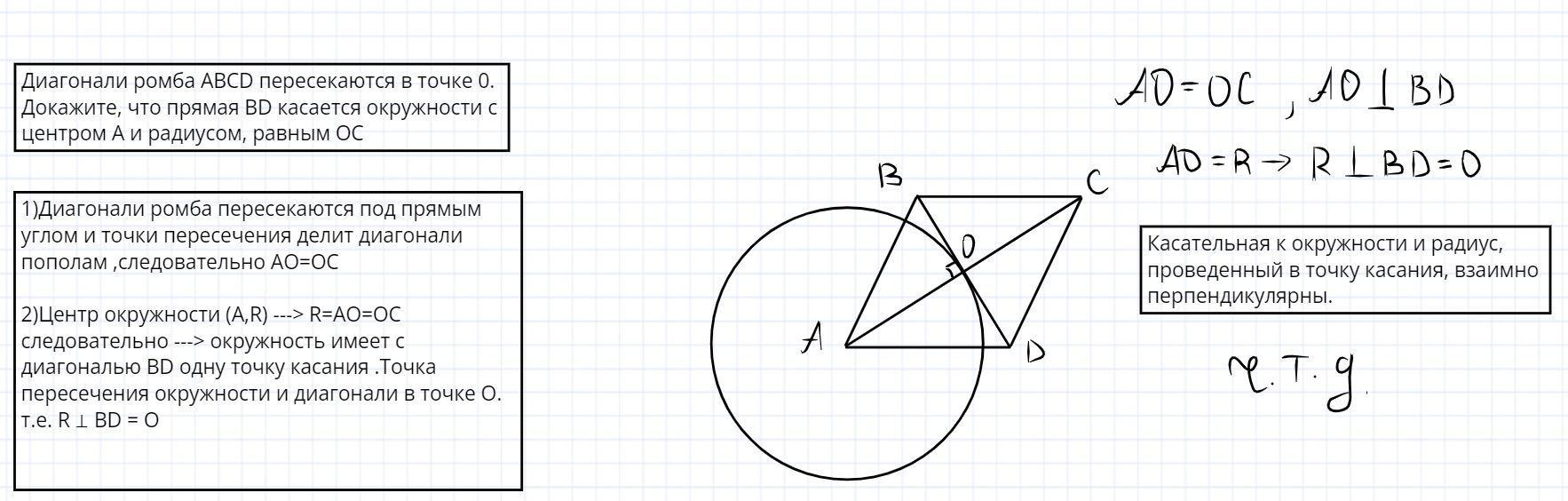
1. Диагонали ромба пересекаются под прямым углом и точки пересечения делит диагонали пополам (по свойству),следовательно AO=OC ⇒

⇒ 2. Центр окружности (А,R) ---> R=AO=OC следовательно ---> oкружность имеет с диагональю BD одну точку касания .Точка пересечения окружности и диагонали в точке О.

т.е. R ⊥ BD = О

т.к. касательная BD к окружности и радиус, проведенный в точку касания, взаимно перпендикулярны.

Касательная к окружности — это прямая, имеющая с ней всего одну общую точку О.