Предмет: Математика
Автор: NoiZy322
Вопрос задан 6 лет назад

< >

Определить тип уравнения. Найти общее решение или решение,
удовлетворяющее заданным начальным условиям

Приложения:

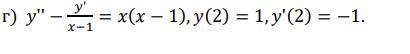
Ответы

Ответ дал: yugolovin

0

Ответ: $y=\dfrac{x^4}{8}-\dfrac{x^3}{6}+C_1\dfrac{(x-1)^2}{2}+C_2;\ y=\dfrac{x^4}{8}-\dfrac{x^3}{6}-\dfrac{3}{2}(x-1)^2+\dfrac{11}{6}.$

Пошаговое объяснение: ${}$ $y''-\dfrac{y'}{x-1}=x(x-1) -$ это линейное неоднородное уравнение 2-го порядка . Поскольку в уравнении в явном виде отсутствует $y,$ можно понизить порядок уравнения, сделав замену

$y'(x)=u(x).$ Но мы пойдем другим путем:

$\dfrac{(x-1)y''-y'}{(x-1)^2}=x; \left(\dfrac{y'}{x-1}\right)'=x;\ \dfrac{y'}{x-1}=\dfrac{x^2}{2}+C_1; y'=\dfrac{x^2(x-1)}{2}+C_1(x-1);$

$y'=\dfrac{x^3}{2}-\dfrac{x^2}{2}+C_1(x-1);\ y=\dfrac{x^4}{8}-\dfrac{x^3}{6}+\dfrac{C_1(x-1)^2}{2}+C_2.$

Это - общее решение. Чтобы найти частное решение, подставим начальные условия в выражения для производной и самой функции. Получаем

$-1=\dfrac{4}{2}+C_1;\ C_1=-3;$

$1=\dfrac{16}{8}-\dfrac{8}{6}+\dfrac{-3}{2}+C_2;\ C_2=\dfrac{11}{6}\Rightarrow$

$y=\dfrac{x^4}{8}-\dfrac{x^3}{6}-\dfrac{3}{2}(x-1)^2+\dfrac{11}{6}.$

Похожие вопросы

Немецкий язык

1 год назад

Пожалуйста помогите с немецким !!!

История

1 год назад

Объясните,почему в Западной Европе Русь иногда называли ,,страной городов''. Заранее спасибо!

Геометрия

2 года назад

В треугольнике авс высоты ак и ве пересекаются в точке О, угол сав=42 градуса. найдите величину угла асо

Русский язык

2 года назад

7..............ЗАПИШИТЕ ТРИ СЛОВА С БЕЗУДАРНОЙ ГЛАСНОЙ В ПАДЕЖНЫХ ОКОНЧАНИЯХ ИМЁН ПРИЛАГАТЕЛЬНЫХ!

Математика

8 лет назад

центнер груш разложили поровну в 5 ящиков. Сколько килограмм груш в каждом ящике?

Химия

8 лет назад

Рассчитайте массу азотной кислоты, необходимой для реакции с 600 г 20%-го раствора гидроксида натрия

Математика

9 лет назад

5. Велосипедист ехал 2,5 ч со скоростью 14км/ч, 1 ч со скоростью 18км/ч и 1,5 часа 24 км. Найдите среднюю скорость велосипедиста за все время движения.

Музыка

9 лет назад

1. Кюй который сочинила Дина Нурпеисова, когда пришло известие о победе над фашмзмом: а)Ананын буйрыгы. б)женыс 2. Автор поэмы "Курмангазы": а)Х.Ергалиев б)Абай Кунанбаев в)М.Ауэзов