Предмет: Геометрия
Автор: angelinnn
Вопрос задан 6 лет назад

< >

Помогите решить пожалуйста с чертежом!!!!

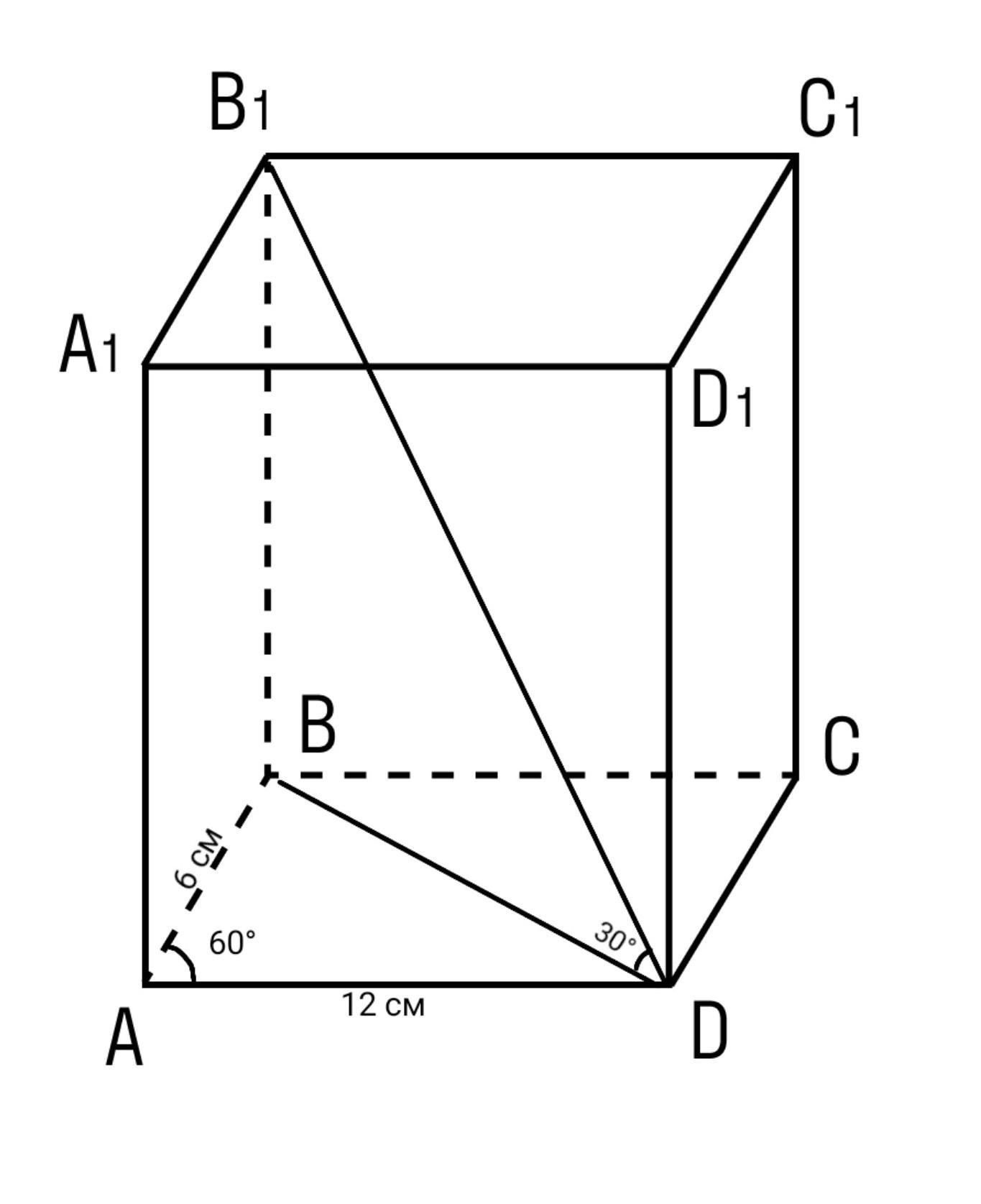
Основанием прямой призмы ABCDA1B1C1D1 является параллелограмм ABCD со сторонами 6 см и 12 см и углом 60°. Диагональ B1D призмы образует с плоскостью основания угол в 30°. Найдите площадь полной поверхности призмы.

Ответы

Ответ дал: bertramjeratire

Ответ:

Площадь полной поверхности:

$S_{полн}=2S_{осн}+S_{бок}$

Основание параллелограмм, поэтому площадь:

$S_{осн} = ab \sin( \alpha )$

$S_{осн} = 6 \times 12 \times \sin( {60}^{ \circ} ) = 6 \times 12 \times \frac{ \sqrt{3} }{2} = 6 \times 6 \sqrt{3} = 36 \sqrt{3}$

Формула площади боковой поверхности: $S_{бок}=P_{осн} \times H$

Нам надо найти высоту H, на рисунке $BB_{1}$

Найдем диагональ основания BD по теореме косинусов:

$BD^{2}=AB^{2}+AD^{2}-AB \times AD \times \cos (\alpha)$

${BD}^{2} = 36 + 144 - 2 \times 6 \times 12 \times \cos( {60}^{ \circ} ) \\ {BD}^{2} = 180 - 2 \times 6 \times 12 \times \frac{1}{2} \\ {BD}^{2} = 180 - 72 \\ {BD}^{2} = 108 \\ BD = \sqrt{108} \\ BD = 6 \sqrt{3}$

В треугольнике ΔBB1D по теореме синусов найдем BB1

$\frac{BD}{\sin(\angle BB_{1}D)} = \frac{BB_{1}}{ \sin( \angle BDB_{1}}$

Угол BB1D=180°-90°-30°=60°

$\frac{6 \sqrt{3} }{ \sin( {60}^{ \circ} ) } = \frac{BB_{1}}{ \sin( {30}^{ \circ} ) }$

$\frac{6 \sqrt{3} }{ \frac{ \sqrt{3} }{2} } = \frac{BB_{1}}{ \frac{1}{2} } \\ BB_{1} = 6$

Теперь можно найти площадь боковой поверхности:

$S_{бок} = 2(6 + 12) \times 6 = 2 \times 18 \times 6 = 32 \times 6 = 192$

Площадь полной поверхности:

$S_{полн} = 2 \times 36 \sqrt{3} + 192 = 72 \sqrt{3} + 192 = 24(3 \sqrt{3} + 8) \: {см}^{3}$

Приложения:

petrovnas21: Неточность в предпоследнем действии: 2*18=36, поэтому ответ: 72(3+√3)

Похожие вопросы

География

1 год назад

я вас умоляю помогите с географией даю все баллы. Ответьте те вопросы которые объведены в круг. буду очень благодарен, спасибо.

Алгебра

1 год назад

Выполните умножение: 1,5x*8x; -a*4a³; 6y*(-⅓y²);

Русский язык

2 года назад

В баснях И.А.Крылова найдите примеры употребления частиц.Выпишите 2-3 предложения.

Алгебра

2 года назад

x/x+5 + x+5/x-5 = 50/x^2-25

География

8 лет назад

Помогите плизз,география 8 класс

Математика

8 лет назад

Начертите отрезки. Длина первого 8 см второй

Математика

9 лет назад

помогите решить уравнение! (40х+14,2)* 35,8=538,79

Математика

9 лет назад

Помогите. А ЭТО РЕШИТЕ? -3,4*8.4*(-1/56)