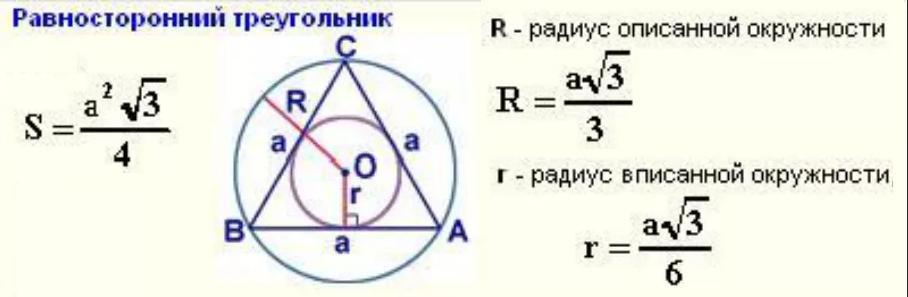
Сторона равностороннего треугольника равна 30√3 см.
Вычисли: площадь треугольника: радиус окружности, вписанной в треугольник: радиус окружности, описанной около треугольника.
S = √3 cм2.
r = см.
R = cм.