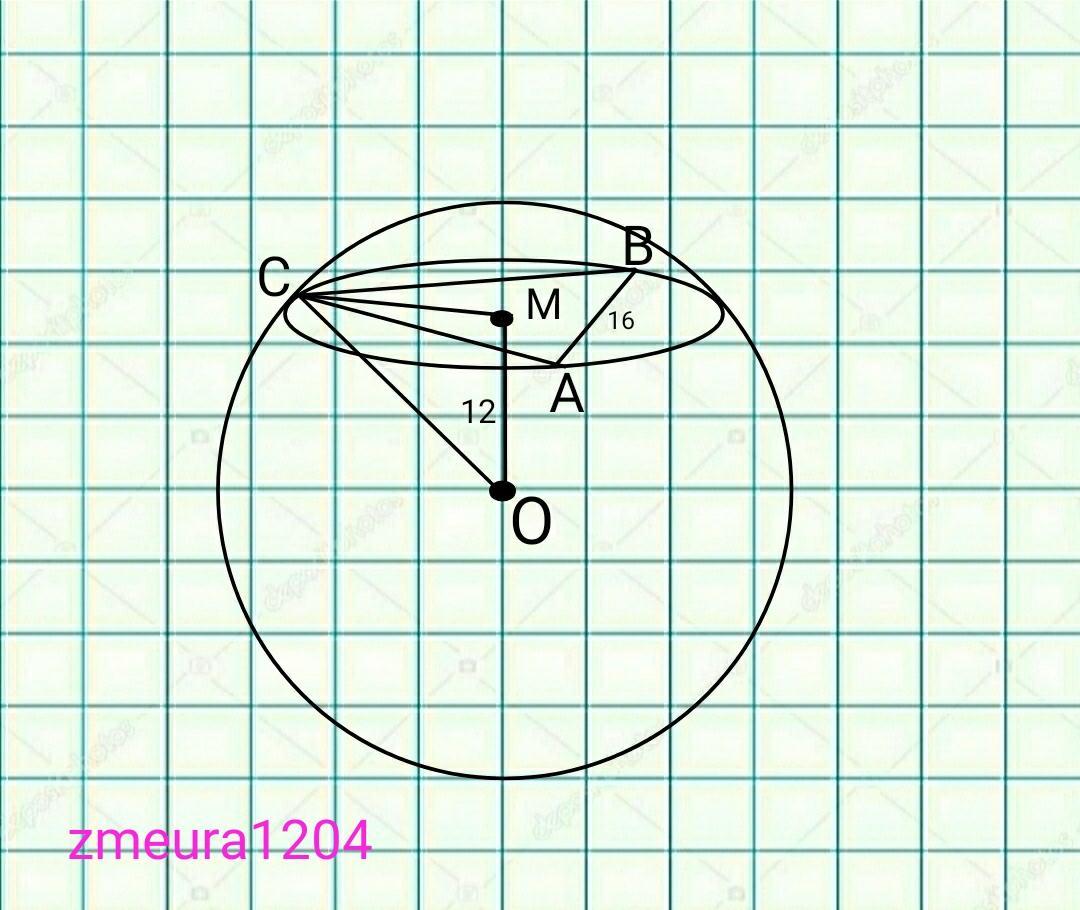
Задан шар. Вершины треугольника ABC лежат на поверхности шара. В ∆ABC AB = 16 см и ∠ C = 150°. Расстояние от центра шара до плоскости треугольника ABC равно 12 см. Найдите радиус шара. Рисунок обязателен.

Ответ:
R=20см

Решение:
r=AB/(2sin∠C), формула нахождения радиуса описанной окружности треугольника.
r=CM;
sin150°=½
CM=16/(2*½)=16 см.

∆CMO- прямоугольный треугольник.
По теореме Пифагора
СО=√(СМ²+МО²)=√(16²+12²)=
=√(256+144)=√400=20см.
R=CM=20см