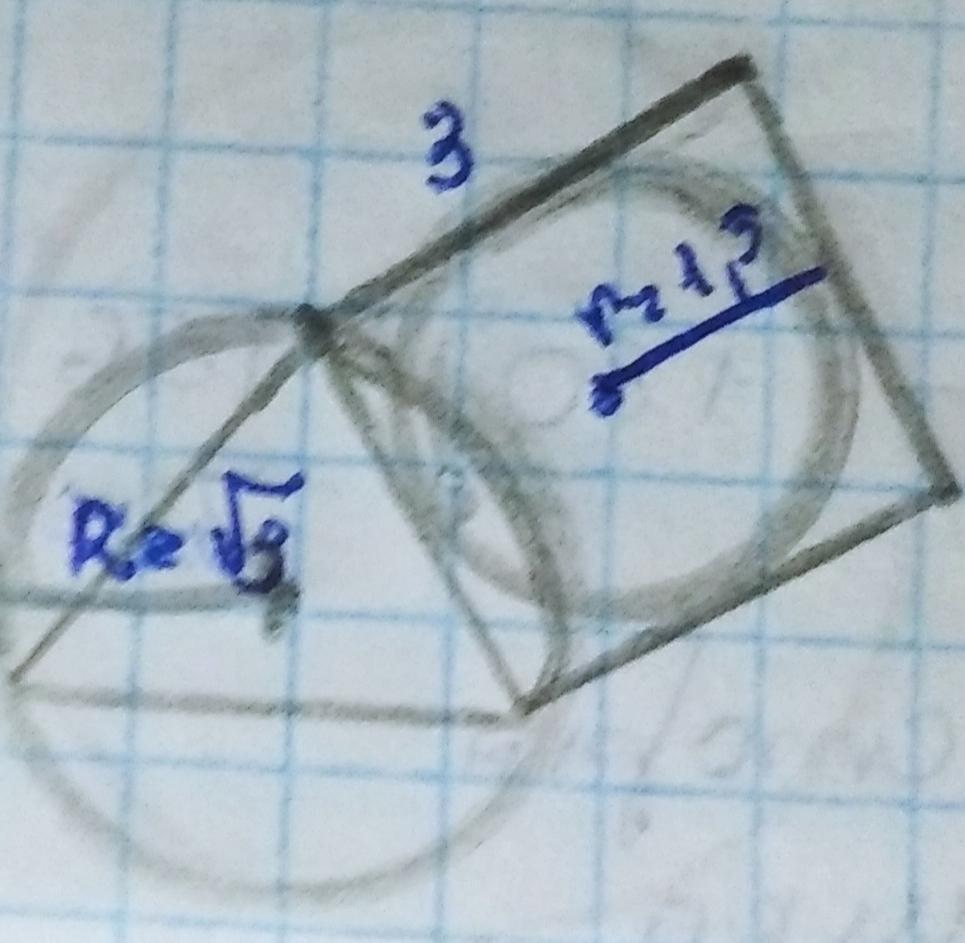
У коло радіуса корінь з трьох см вписано правильний трикутник. На його стороні побудовано квадрат у який вписане коло. Знайти площу круга, обмеженого цим колом.

Ответы

Ответ дал: sofiaklimcuk00

Ответ:

S = 2.25π.

Объяснение:

Sкруга = πr²

Знайдемо сторону квадрата:

Оскільки сторона квадрата є стороною правильного трикутника (умова задачі), то ми будемо шукати сторону трикутника через радіус описаного навколо нього кола. Для цього візьмемо формулу знаходження радіусу описаного кола - R₃= $\frac{a\sqrt{3} }{3}$ . За цією формулою знаходиться радіус, який нам вже даний, тому з неї ми можемо знайти а (а - кількість сторін правильного n-кутника). Отже, тепер у нас формула буде у такому вигляді: а = $\frac{R3 *3}{\sqrt{3} }$ ( * - це множення). Підставивши значення отримаємо: а = $\frac{\sqrt{3} * 3 }{\sqrt{3} }$ = 3.

Отже, сторона квадрата 3 см. Оскільки, коло вписане в квадрат то, радіус(r) цього кола, буде дорівнювати половині сторони квадрата, тобто, r = 1.5 см.

Тоді, ми можемо знайти площу круга( круг - це геометрична фігура, обмежена колом, тобто, серединка кола.) (π≈3,14, якщо потрібна конкретна відповідь, просто потрібно буде 2,25*3,14).

S = πr²= π * (1,5)² = 2,25П.

Бажаю успіхів! Сподіваюсь зрозуміли моє пояснення)

Малюночок до задачі :

Приложения: