Предмет: Алгебра
Автор: mekanur
Вопрос задан 6 лет назад

Решить тригонометрическое уравнение

Приложения:

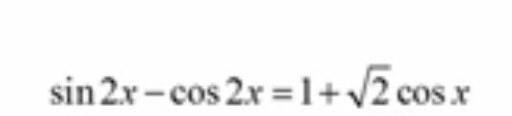
Simba2017: могу решить, но только в комментариях-решать?

Ответы

Ответ дал: kamilmatematik100504

Ответ:

$\left [ \begin{array} {l} \dfrac{\pi }{2} +\pi n \\\\ (-1)^{n+1}\cdot \dfrac{\pi }{12}+ \dfrac{\pi n}{2}~~ , ~ n \in \mathbb {Z} \end{array}$

Объяснение:

$\displaystyle \sin 2x - \cos 2x= 1+\sqrt{2} \cos x \\\\$

Воспользуемся формулами

$\sf cos ~ 2a = cos^2 a -sin^2a \\\\ sin~2a= 2~ sin ~a\cdot cos ~a$

Тогда

$\displaystyle \sin 2x - \cos 2x= 1+\sqrt{2} \cos x\\\\ 2\sin x \cos x - (\cos ^2x- \sin^2x)=\sin ^2x+\cos ^2x +\sqrt{2} \cos x \\\\ 2\sin x\cos x-\cos^2x+\sin ^2x =\sin^2+\cos^2x+\sqrt{2} \cos x \\\\ 2\cos ^2x+\sqrt{2}\cos x-2\sin x\cos x =0 \\\\ 2\cos x\bigg (\cos x-\sin x + \frac{\sqrt{2} }{2} ~ \bigg ) =0$

Каждую скобку приравняем к нулю

$1) ~~ \cos x = 0 \Leftrightarrow\boxed{ x = \frac{\pi }{2} +\pi n~~ , ~ n \in \mathbb Z}$

$\displaystyle \hspace{-1em} 2) ~ \cos x -\sin x+\dfrac{\sqrt{2} }{2} =0 \\\\ (\cos x-\sin x)^2 =\bigg(-\cfrac{\sqrt{2} }{2} ~ \bigg )^2 \\\\ \sin ^2x+\cos ^2 x -2 \sin x\cos x = \cfrac{1}{2} \\\\ 1-\sin 2x =\cfrac{1}{2} \\\\ \sin 2x =\frac{1}{2} \\\\ 2x =(-1)^{n+1}\arcsin \frac{1}{2} +\pi n \\\\ 2x =(-1)^{n+1} \cdot \cfrac{\pi }{6} +\pi n \\\\ \boxed{x =(-1)^{n+1}\cdot \frac{\pi }{12}+ \frac{\pi n}{2}~~ , ~ n \in \mathbb Z }$