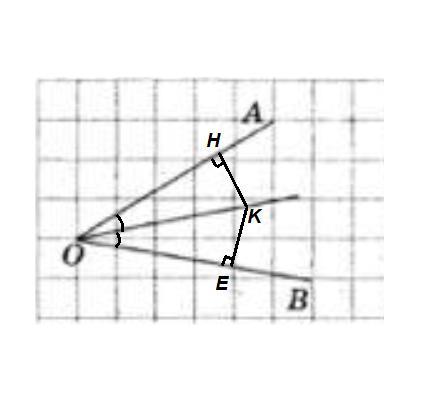
5. Використовуючи рисунок, доведіть, що точка, яка лежить на бісектрисі
кута АОВ, розташована на однаковій відстані від прямих АО і ВО.

Ответ:

• Расстоянием от точки до прямой называется длина перпендикуляра, проведенного из точки к прямой.

Из произвольной точки К, лежащей на биссектрисе угла АОВ, проведем перпендикуляры к сторонам угла:

КН⊥ОА и КЕ⊥ОВ.

Рассмотрим треугольники ОКН и ОКЕ:

• ∠ОНК = ∠ОЕК = 90°;
• ∠КОН = ∠КОЕ, так как ОК - биссектриса;
• ОК - общий катет,

значит ΔОКН = ΔОКЕ по катету и прилежащему острому углу.

• В равных треугольниках против равных сторон лежат равные углы, значит

КН = КЕ.

То есть точка, которая лежит на биссектрисе угла АОВ, расположена на одинаковом расстоянии от прямых ОА и ОВ.