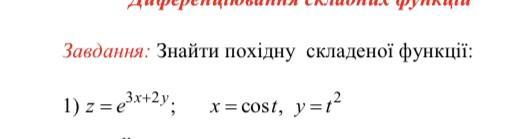• Предмет: Математика
  • Автор: KatyaBrovko17
  • Вопрос задан 6 лет назад
< >

Знайти похідну складеної функції z=e^3x+2y, x=cost y=t^2
Допоможіть будь ласкааа

Приложения:

Ответы

Ответ дал: pushpull
3

Ответ:

\displaystyle \boldsymbol { \frac{dz}{dt} =e^{3x+2y}(4t-3sin(t)}

Пошаговое объяснение:

Формула для нахождения производной сложной функции нескольких переменных

\displaystyle \frac{dz}{dt} =\frac{\delta z}{\delta x} *\frac{\delta x}{\delta t} +\frac{\delta z}{\delta y} *\frac{\delta y}{\delta t}

\displaystyle z=e^{3x+2y}\quad x=cos(t)\qquad y=t^2

Найдем все наши "части"

\displaystyle \frac{\delta z}{\delta x} =3e^{3x+2y};\qquad \frac{\delta x}{\delta t} =-sin(t)\\\\\\\frac{\delta z}{\delta y} =2e^{3x+2y};\qquad \frac{\delta y}{\delta t} =2t

Теперь запишем производную

\displaystyle \frac{dz}{dt} =-3e^{3x+2y}sin(t)+4te^{3x+2y}=e^{3x+2y}(4t-3sin(t)

Похожие вопросы
Литература
1 год назад
Как звали главного героя сказки В.Гауфа? Почему его так назвали? Какие события с ним приключились?
Русский язык
1 год назад
сочинение-миниатюра Представьте себе, что вы превратились в какой-либо предмет (компьютер, автомобиль, куст сирени…). Опишите, что вы чувствуете, о чем думаете, о чем мечтаете. Постарайтесь
Русский язык
2 года назад
10 городов рек озёр в мн.ч
Українська мова
2 года назад
Скласти поширений діалог на будь-яку тему з займенниками .СРОЧНО ПОСТАВЛЮ ЛУТШОЕ
Химия
8 лет назад
химия. выберите изомеры и гомологи) определите класс веществ) Хотя бы парочку, пожалуйста))
Математика
8 лет назад
конечная числовая последовательность содержит 10 членов, первый из которых равен 1,а каждый последующий член, начиная со второго, больше предыдущего в два раза. Найдите шестой член последовательности
Биология
9 лет назад
Какие органоиды отсутствуют в клетке человека и животных?
История
9 лет назад
1. Что из названного характерно для преобразований Петра I? o 1)европеизация культуры и быта o 2)создание сословно-представительных органов o 3)начало ограничения крепостничества