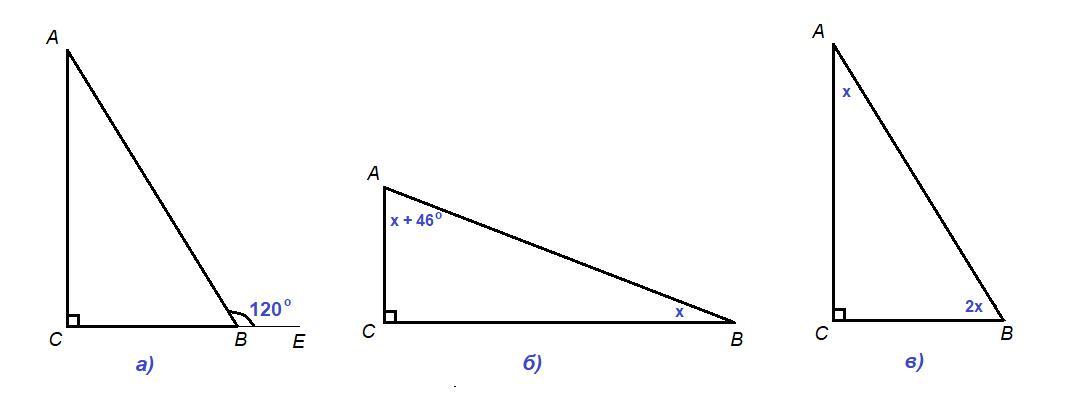
найдите острые углы прямоугольного треугольника если а) один из внешних углов треугольника равен 120°, б)один из них больше второго на 46°,в) один из них меньше в 2 раза, пожалуйста помогите срочно

Ответ:

1.

а) 30° и 60°;

б) 22° и 68°;

в) 30° и 60°.

11. PQ = 14.

Объяснение:

а) Внешний угол треугольника - угол, смежный с внутренним, их сумма равна 180°.

∠АВС + ∠АВЕ = 180°

∠АВС = 180° - ∠АВЕ = 180° - 120° = 60°

• Сумма острых углов прямоугольного треугольника равна 90°.

∠А = 90° - ∠АВС = 90° - 60° = 30°

б) Пусть ∠В = х, тогда ∠А = х + 46°

По свойству острых углов прямоугольного треугольника:

∠В + ∠А = 90°

x + x + 46° = 90°

2x = 90° - 46°

2x = 44°

x = 22°

∠B = 22°

∠A = 22° + 46° = 68°

в) Пусть ∠А = х, тогда ∠В = 2x

По свойству острых углов прямоугольного треугольника:

∠А + ∠В = 90°

x + 2x = 90°

3x = 90°

x = 30°

∠А = 30°

∠В = 2 · 30° = 60°

11. ΔPRQ - равнобедренный, значит углы при основании равны:

∠RPQ = ∠PRQ

Так как сумма углов треугольника равна 180°, то

∠RPQ = ∠PRQ = (180° - ∠PRQ) : 2 = (180° - 120°) : 2 = 60° : 2 = 30°

В прямоугольном треугольнике PSQ ∠Q = 30°, тогда

PQ = 2 · PS = 2 · 7 = 14 по свойству катета, лежащего против угла в 30°.