вычислить двойной интеграл, используя полярные координаты
Приложения:
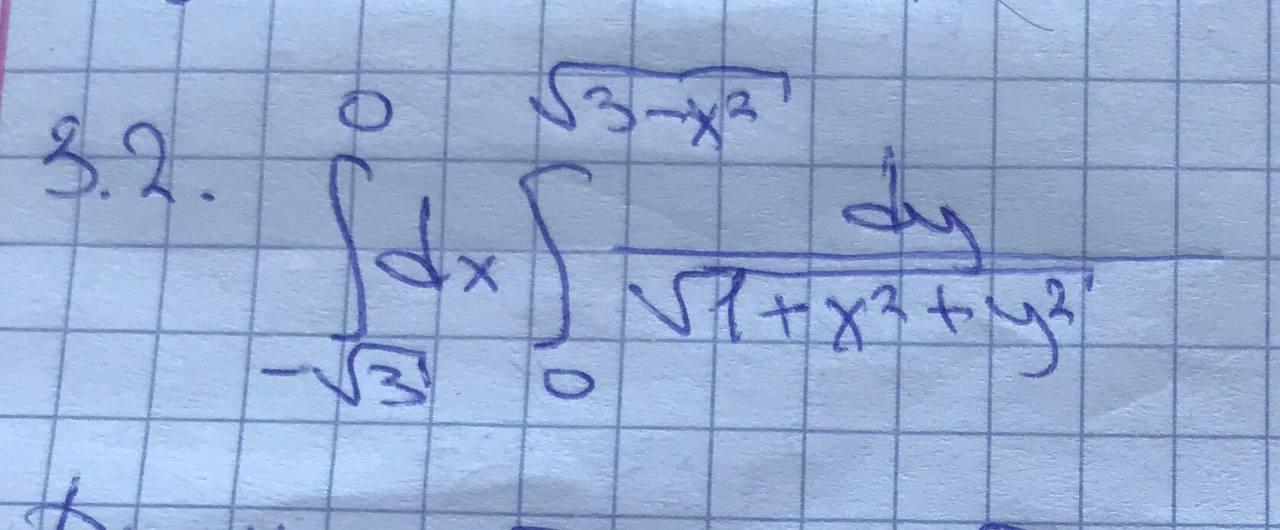
pushpull:
здесь знаменатель правильный? не 1 + √(x²+y²) ?
правильный
Ответы
Ответ дал:
0
Ответ:
Пошаговое объяснение:
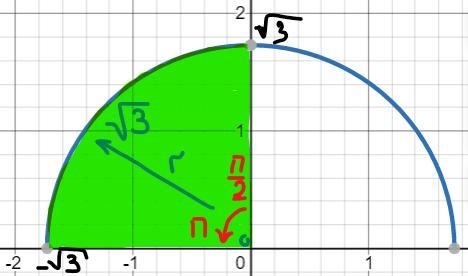
Перейдем к полярной системе координат:
x=r cosφ, y=r sinφ
На рисунке изображена область (зеленая), по которой происходит интегрирование. При переходе к полярным координатам область интегрирования переходит в область r∈[0;√3], φ∈[π/2;π]. А интеграл преобразуется в следующий:
При вычислениях воспользовался следующим:
1) под первым интегралом стоит функция, независящая от φ, значит один интеграл по φ = длине отрезка интегрирования = π/2
2) Воспользовался стандартым интегралом, который находится с помощью замены r=tg t:
Приложения:
Похожие вопросы
1 год назад
1 год назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад
9 лет назад