Предмет: Алгебра
Автор: annagreshanuyk
Вопрос задан 6 лет назад

< >

нужна помощь срочная

Приложения:

Ответы

Ответ дал: mzyr657

1

Ответ:

я решила я решила я решила

Приложения:

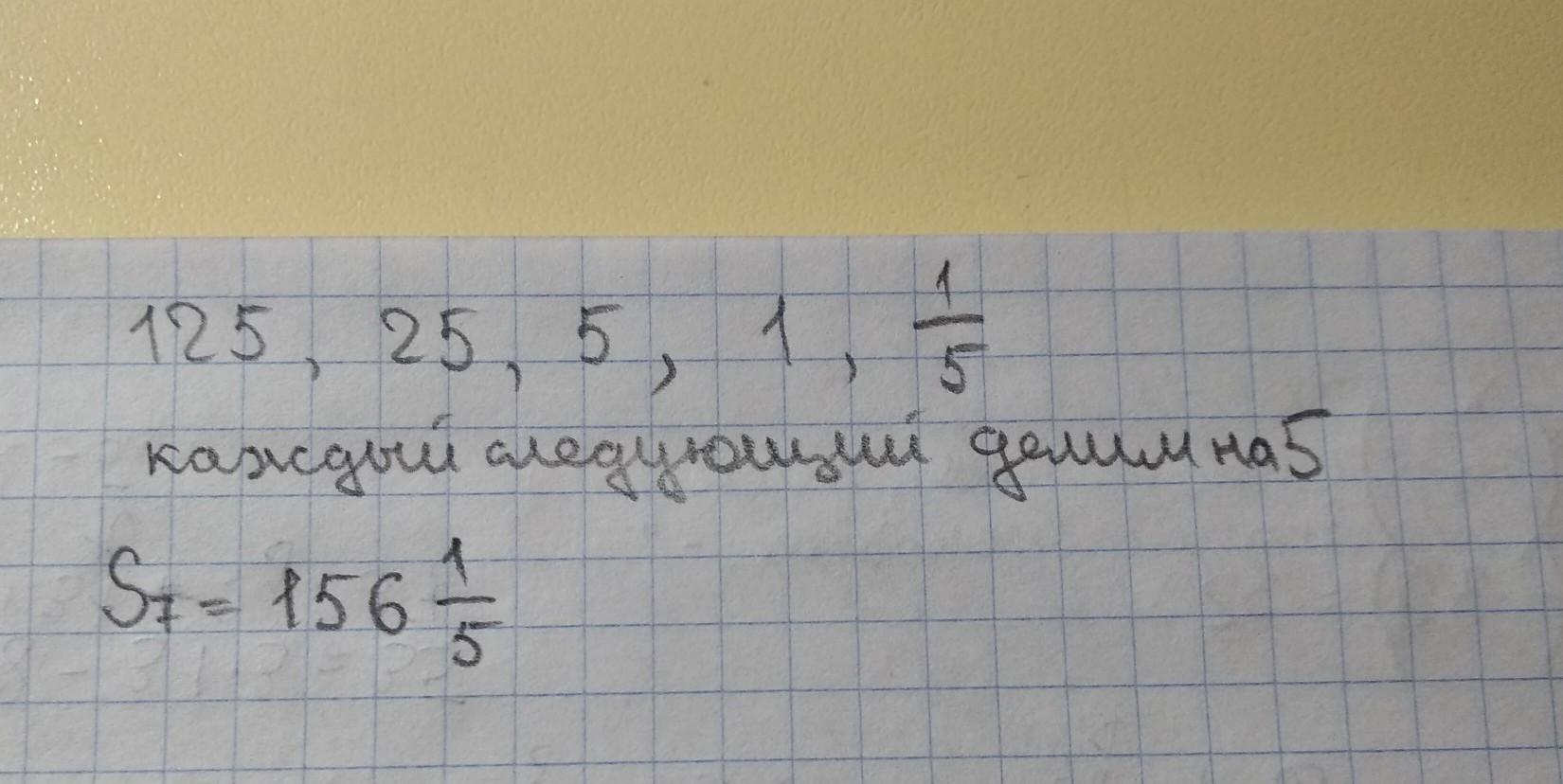
Ответ дал: nafanya2014

0

$b_{n}=b_{1}\cdot q^{n-1}$ - формула n-го члена геометрической прогрессии

$b_{2}=b_{1}\cdot q$ ⇒ $25=b_{1}\cdot q$

$b_{5}=b_{1}\cdot q^4$ ⇒ $\frac{1}{5} =b_{1}\cdot q^4$

Решаем систему двух уравнений:

$\left \{ {{25=b_{1}\cdot q} \atop {\frac{1}{5} =b_{1}\cdot q^4}} \right.$

$\left \{ {{b_{1}=\frac{25}{q}} \atop {\frac{1}{5} =\frac{25}{q}\cdot q^4}} \right.$

$\left \{ {{b_{1}=\frac{25}{q}} \atop {q^3=\frac{1}{125} }} \right.$

$\left \{ {{b_{1}=\frac{25}{\frac{1}{5}}} \atop {q=\frac{1}{5} }} \right.$

$\left \{ {{b_{1}=125} \atop {q=\frac{1}{5} }} \right.$

По формуле:

$S_{7}=\frac{b_{1}\cdot (1-q^{7})}{1-q}$

$S_{7}=\frac{125\cdot (1-(\frac{1}{5})^{7})}{1-\frac{1}{5}}$

$S_{7}=\frac{125-\frac{125}{5^7}}{\frac{4}{5}}$

$S_{7}=\frac{125\cdot 5-\frac{5^4}{5^7}}{4}$

$S_{7}=\frac{625-\frac{1}{125}}{4}$

$S_{7}=\frac{624\frac{124}{125}}{4}\\\\S_{7}=156\frac{31}{125}$

2 способ.

Найти семь членов геометрической прогрессии

$a_{1}=125\\\\a_{2}=a_{1}\cdot \frac{1}{5}=125\cdot \frac{1}{5}=25 \\\\a_{3}=a_{2}\cdot \frac{1}{5}=25\cdot \frac{1}{5}=5\\\\a_{4}=1\\\\a_{5}=\frac{1}{5}\\\\a_{6}=a_{5}\cdot \frac{1}{5}=\frac{1}{5}\cdot \frac{1}{5}=\frac{1}{25}\\\\a_{7}=a_{6}\cdot \frac{1}{5}=\frac{1}{25}\cdot \frac{1}{5}=\frac{1}{125}$

и сложить

$S_{7}=125+25+5+1+\frac{1}{5}+\frac{1}{25} +\frac{1}{125}=156\frac{31}{125}$

О т в е т. $S_{7}=156\frac{31}{125}$

Похожие вопросы

Українська мова

1 год назад

Сьогодні у нас теж відбувається війна і ця війна іде впродовж чотирьох років.В цьому випадку перед і треба ставити кому чи не треба?

Окружающий мир

1 год назад

отрасль сельского хозяйства которая больше всех развита в москве

Английский язык

2 года назад

Необходимо ответить на вопросы в конце текста. Помогите, пожалуйста) Survey The simplest and most commonly used method of measuring the distance between two points on the ground is called chain

Русский язык

2 года назад

ПОМОГИТЕ ПОЖАЛУЙСТА!!!! Синтаксический разбор простого предложения. где между тем некому велеть зажарить фазана и сварить щей.

Алгебра

8 лет назад

7 класс. Решите задачу номер 2, пожалуйста

Литература

8 лет назад

Помогите Срочно!!!!! Лермонтов.Ашик Кериб. Отметь ✓ правильный вариант ответа.

История

9 лет назад

справедливо ли нерона прозвали кровавым императором?Свой ответ обьясните.

Математика

9 лет назад

Из одного лагеря в противоположных направлениях вышли две группы туристов. Через 0,4 ч расстояние между ними было 3,88 км. Найдите скорость движения второй группы, если первая группа двигалась со