Помогите пожалуйста номер 12. 14

Ответ:

Объем призмы      равен 30см³

Объяснение:

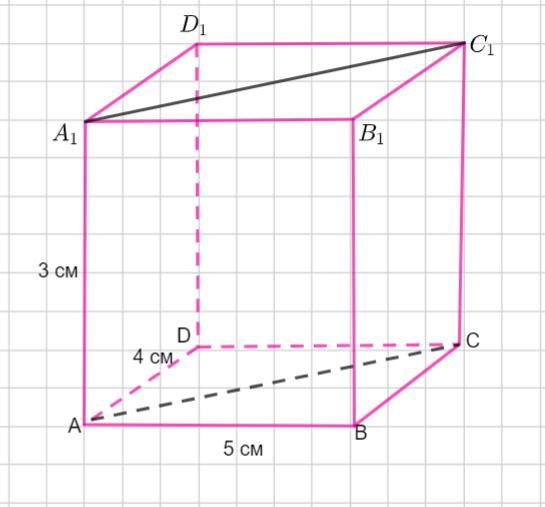
По условию задан прямоугольный параллелепипед

Три ребра, выходящие из одной вершины равны 5 см, 4 см и 3 см.

Надо найти объем треугольной призмы .

Объем призмы  определяется по формуле:

где S- площадь основания, а  H-  высота призмы.

Высота призмы дана по условию Н=3 см.

Найдем площадь основания, то есть площадь прямоугольного ΔАВС, как полупроизведение катетов.

Площадь основания призмы равна 10 см². Тогда получим объем

см³.