Срочно помогите,даю много баллов

Приложения:

Ответы

Ответ дал: hote

Напомню таблицу производных

$\displaystyle sin`x=cosx\\\\cos`x=-sinx$

тогда

$\displaystyle f(x)=-cosx\\\\\int -cosx dx=-\int cosxdx=-sinx+C\\\\f(x)=-sinx\\\\\int-sinxdx=-\int sinxdx=-(-cosxc)+C=cosx+C\\\\f(x)=cosx\\\\ \int cosxdx=sinx+C$

Ответ дал: NNNLLL54

Ответ:

$\displaystyle \int f(x)\, dx=F(x)+C$

По таблице интегралов имеем:

$\displaystyle \int cosx\, dx=sinx+C\ \ ,\ \ \ \int sinx\, dx=-cosx+C$ .

Поэтому $\displaystyle \int (-cosx)\, dx=-sinx+C\ \ ,\ \ \ \int (-sinx)\, dx=cosx+C$ .

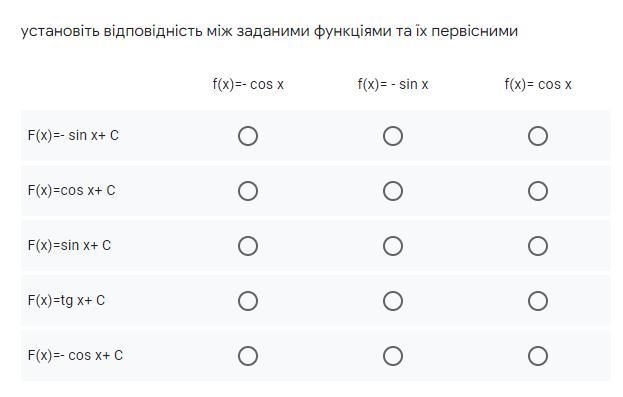
Соответствие между заданными функциями и первообразными смотри в таблице .

Приложения:

Похожие вопросы

Русский язык

1 год назад

составь текст на тему экскурсия в музей слова-помощники: кассы ,билет ,картины, живопись ,зал, Исаак Ильич Левитан ,Алексей Кондратьевич Саврасов, Абильхан Кастеев ,Айша Алимбаева. ПОМОГИТЕ ПЖ даю

Английский язык

1 год назад

помогите даю 20 БАЛОВ !!!)) У МЕНЯ СЕГОДНЯ ДНЮХА !!! ПЖЖЖЖЖ

Русский язык

2 года назад

краткое сочинение "что нужно что люди друг друга понимали"?

Українська мова

2 года назад

Провїдмїняйте словосполучення -1 електронна пошта 2 дорожнї знаки 3 безпечне перехрестя 4 вхїднї повїдомлення

Алгебра

8 лет назад

Помогите пожалуйста !!!!!!

Математика

8 лет назад

решите неопределенный интеграл, пожалуйста, подробнее

Математика

9 лет назад

напишите задачи,которые решаются диаграммой

География

9 лет назад

исправить географические ошибки в дневнике