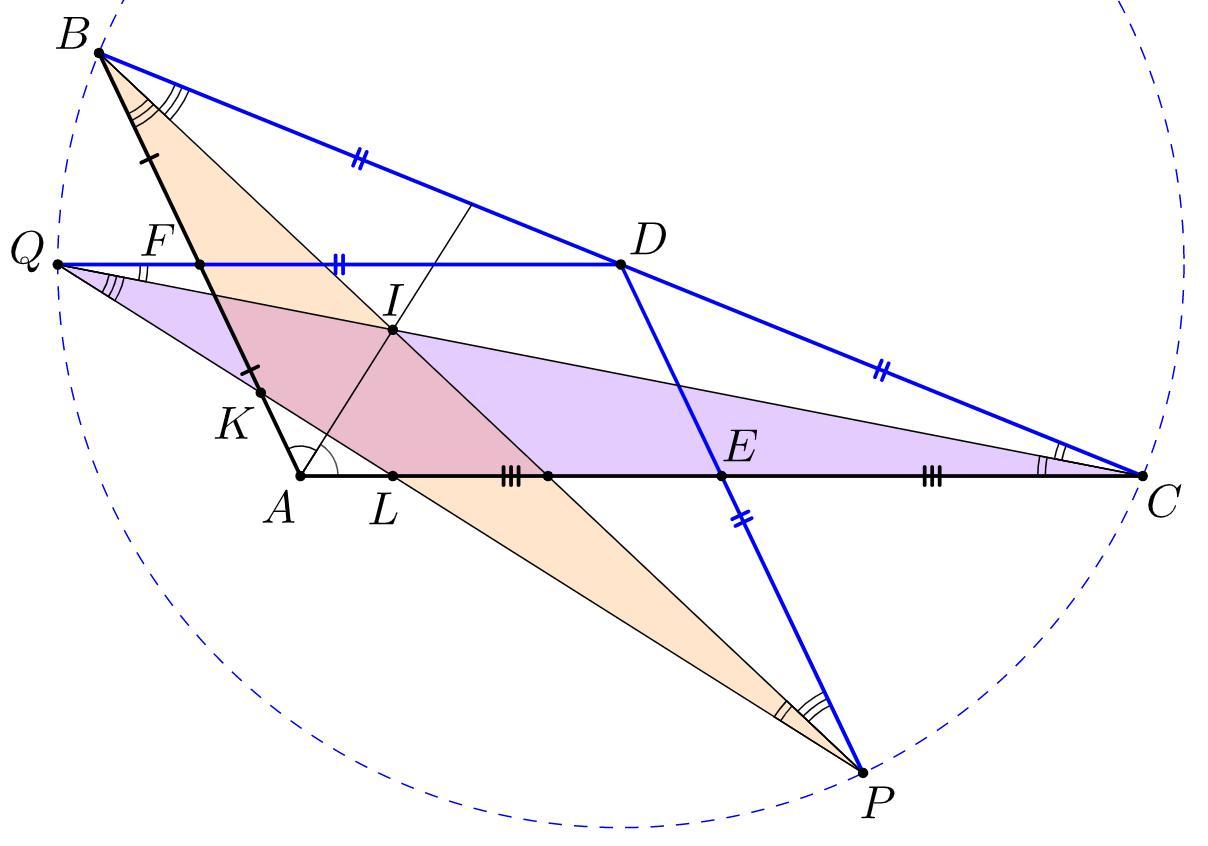
Дан треугольник ABC, биссектрисы которого пересекаются в точке I. Точки D, E, F − середины сторон BC, AC, AB соответственно. P − точка пересечения прямых BI и DE, Q − точка пересечения прямых CI и DF. Прямая PQ пересекает стороны AB и AC в точках K и L соответственно. Докажите, что треугольник AKL − равнобедренный.

Ответ: ч.т.д.

Объяснение:

1) (как средняя линия), следовательно как накрест лежащие, значит и - равнобедренный,

2) (как средняя линия), следовательно как накрест лежащие, значит и - равнобедренный,

3) , значит около можно описать окружность с центром в точке

4) , как вписанные углы, опирающиеся на одну дугу

5) , как вписанные углы, опирающиеся на одну дугу

6) (как внешний угол )

7) (как внешний угол )

8) , следовательно - равнобедренный, поскольку у него равны углы при основании