СРОЧНО!!!!! Накресліть трикутник АВС. Побудуйте образ трикутника АВС: а) при повороті навколо точки В на 120˚ за годинниковою стрілкою; б) при симетрії відносно прямої АС; в) при симетрії відносно точки О, що лежить поза трикутником.

Ответ:

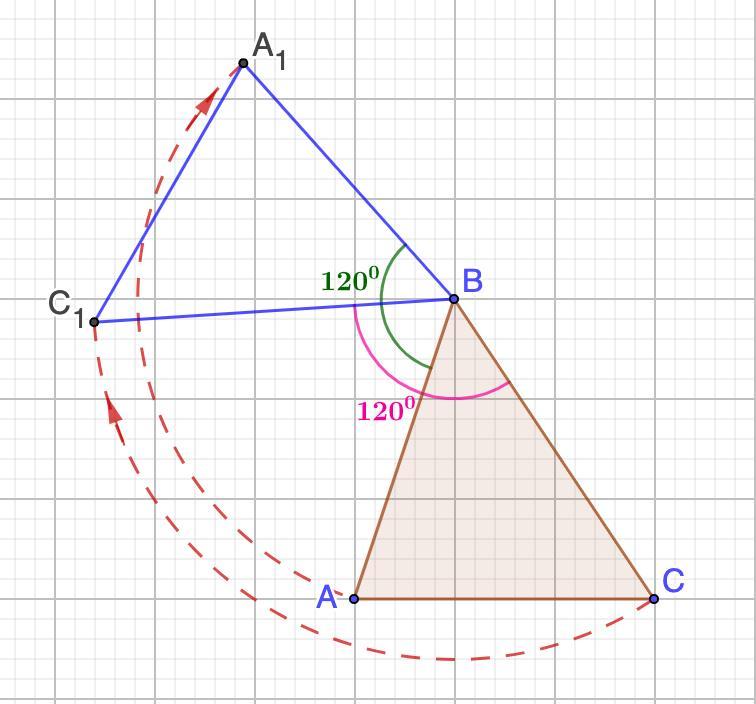
а) Построили ΔС₁А₁В, который является образом треугольника АВС при повороте вокруг точки В на 120° по часовой стрелке.

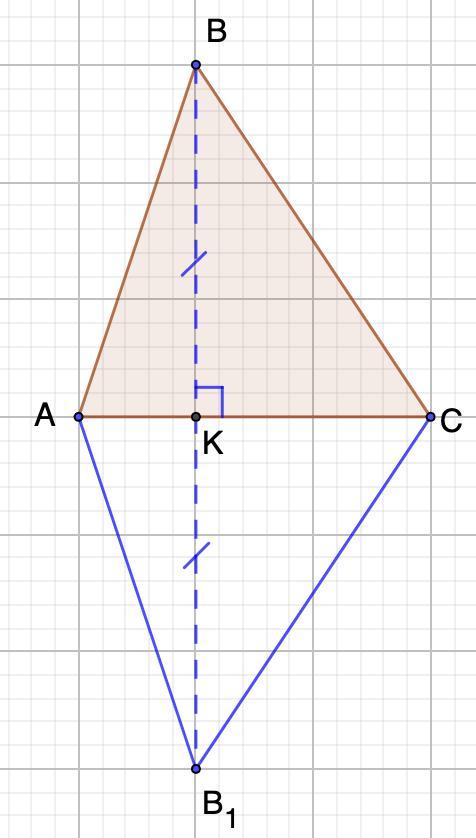
б) Построили ΔАСВ₁, который является образом треугольника АВС при симметрии относительно прямой АС.

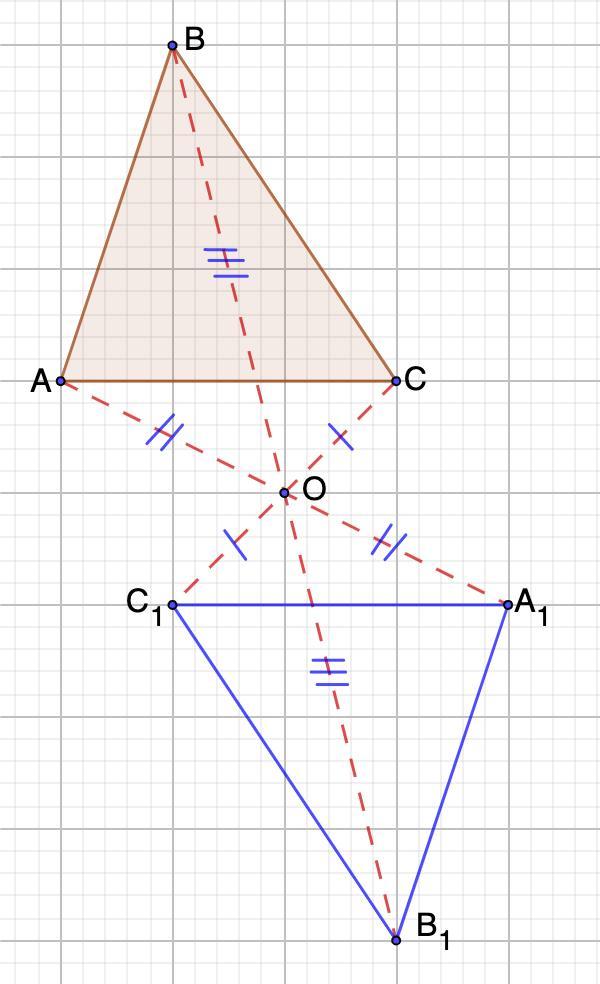
в) Построили ΔС₁А₁В₁, который является образом треугольника АВС при симметрии относительно точки О, лежащей вне треугольника.

Объяснение:

Начертить треугольник АВС. Построить образ треугольника АВС:

а) при повороте вокруг точки В на 120° по часовой стрелке;

б) при симметрии относительно прямой АС;

в) при симметрии относительно точки О, лежащей вне треугольника.

а) Построим образ треугольника АВС при повороте вокруг точки В на 120° по часовой стрелке.

Точка В остается на месте.

Вершины А и С повернем по часовой стрелке на 120° вокруг вершины В. Получим точки А₁ и С₁ соответственно.

Соединим точки В, А₁ и С₁.

Получили ΔС₁А₁В, который является образом треугольника АВС при повороте вокруг точки В на 120° по часовой стрелке.

б) Построим образ треугольника АВС при симметрии относительно прямой АС.

• Две точки А и А1 называются симметричными относительно прямой а, если эта прямая проходит через середину отрезка АА1 и перпендикулярна к нему.

• Если точка А лежит на прямой а, то она симметрична сама себе относительно прямой а.

Точки А и С лежат на прямой АС, поэтому они симметричны сами себе.

Остается построить точку В₁, симметричную точке В относительно АС.

Для этого проведем ВК ⊥ АС. На продолжении луча ВК отложим отрезок, равный ВК и поставим точку В₁.

Соединим точки А, С и В₁.

Получили ΔАСВ₁, который является образом треугольника АВС при симметрии относительно прямой АС.

в) Построить образ треугольника АВС при симметрии относительно точки О, лежащей вне треугольника.

Отметим произвольную точку О, лежащую вне ΔАВС.

• Две точки А и А₁ симметричны относительно точки О, если О– середина отрезка АА₁.

Последовательно соединим точки А, В и С с точкой О и отложим на продолжении лучей АО, ВО и СО отрезки, равные АО, ВО и СО соответственно. Поставим точки А₁, В₁ и С₁.

Соединим точки А₁, В₁ и С₁.

Получили ΔС₁А₁В₁, который является образом треугольника АВС при симметрии относительно точки О, лежащей вне треугольника.