В прямоугольном треугольнике с острым углом 40° проведены три биссектрисы. Вычислите углы, под которыми они пересекаются.​

Ответ:

∠АОС=110°, ∠АОВ=135°, ∠ВОС=115°.

Объяснение:

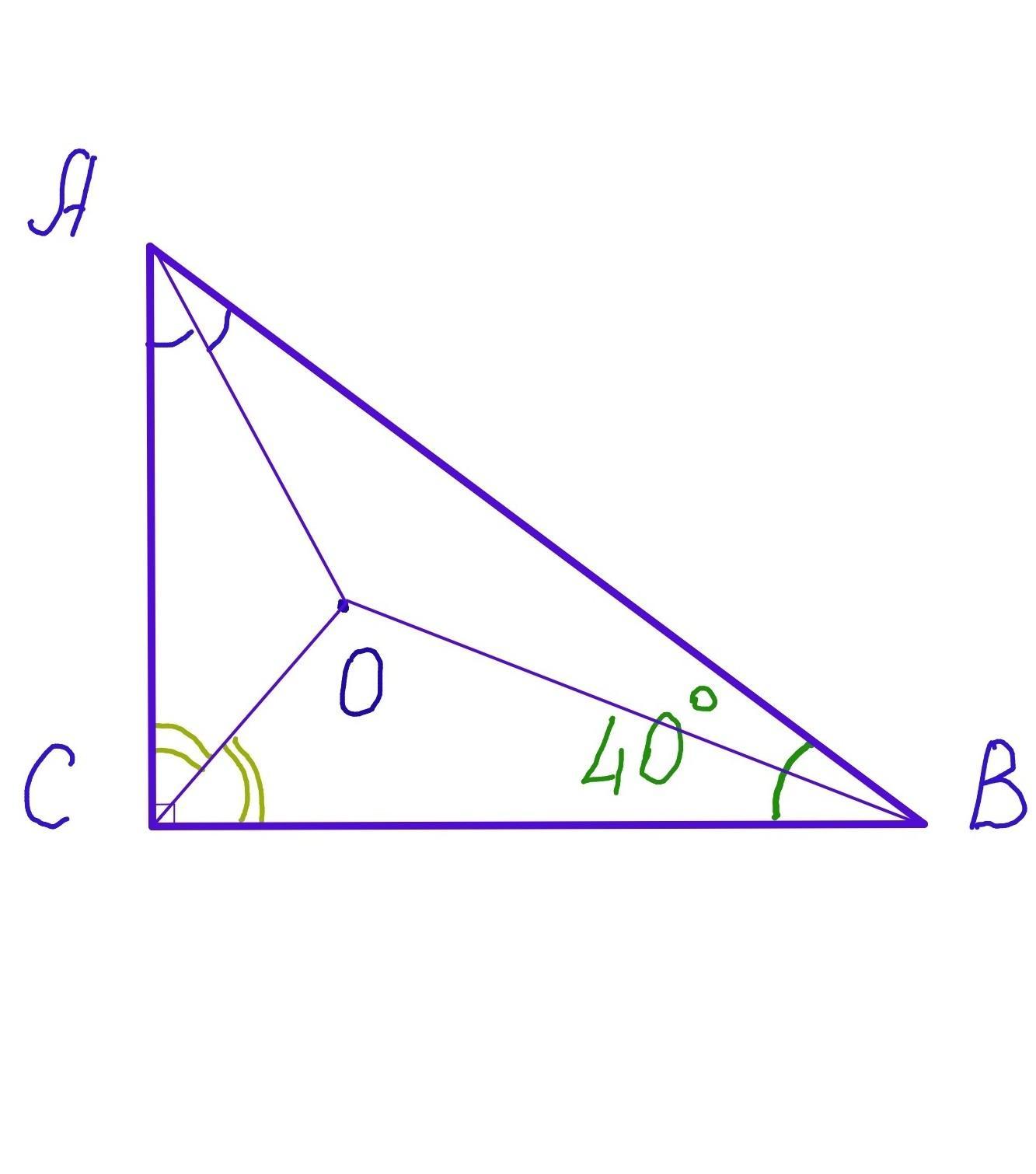
Дан прямоугольный треугольник АВС (∠С=90°). ∠В=40°. АО, ВО, СО - биссектрисы соответственно углов ∠А, ∠В, ∠С. Найдём углы, под которыми они пересекаются: ∠АОС, ∠АОВ, ∠ВОС.

Решение.

По свойству острых углов прямоугольного треугольника ∠А=90°-∠В=90°-40°=50°.

• Биссектриса угла треугольника - это луч, исходящий из вершины угла треугольника и делящий этот угол на два равных угла.

Следовательно:

∠САО=∠ВАО=½•∠А=½•50°=25°

∠АВО=∠СВО=½•∠В=½•40°=20°

∠АСО=∠ВСО=½•∠С=½•90°=45°

• Сумма углов треугольника равна 180°.

Рассмотрим △ АОС.

∠АОС=180°-∠САО-∠АСО=180°-25°-45°=110°

Рассмотрим △ АОВ.

∠АОВ=180°-∠ВАО-∠АВО=180°-25°-20°=135°

Рассмотрим △ ВОС.

∠ВОС=180°-∠СВО-∠ВСО=180°-20°-45°=115°