ПОЖАЛУЙСТА, ПОМОГИТЕ МНЕ ДЕБИЛУ!!!
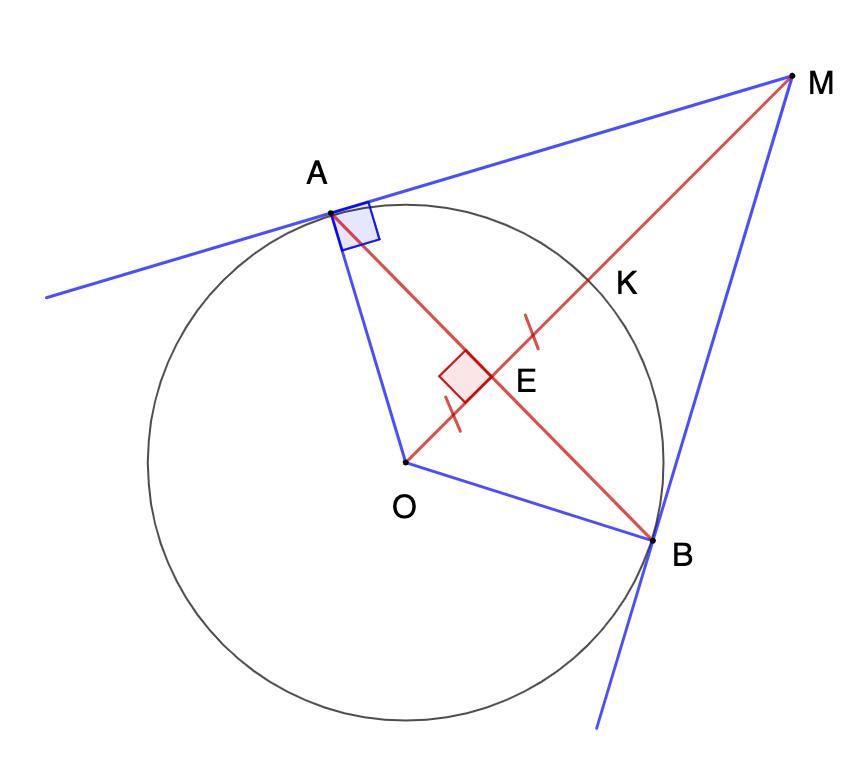
Через точку М, лежащую вне окружности с центром О, проведены касательные МА и МВ к окружности (А и В - точки касания). Отрезок Ом пересекает окружность в точке К. Известно, что прямая АВ делит отрезок ОК пополам. В каком отношении точка К делит отрезок МО?

Ответ:

Точка К делит отрезок МО в отношении 1 : 1.

Пошаговое объяснение:

Определить, в каком отношении точка К делит отрезок МО.

Дано: Окр,О;

МА и МВ - касательные;

А и В - точки касания;

Окр,О ∩ ОМ = К

ОК ∩ АВ = Е; ОЕ = ЕК;

Найти: ОК : КМ.

Решение:

1. Рассмотрим ΔАМВ.

• Отрезки касательных к окружности, проведенные из одной точки, равны.

⇒ АМ = МВ.

ΔАМВ - равнобедренный.

• Центр вписанной окружности лежит на биссектрисе угла.

⇒ МЕ - биссектриса.

• В равнобедренном треугольнике биссектриса, проведенная к основанию, является высотой.

⇒ МЕ ⊥ АВ.

2. Рассмотрим ΔОАЕ - прямоугольный.

ОА = OK = R;

OE = EK (условие)

⇒ ОЕ = R/2

• Если в прямоугольном треугольнике катет равен половине гипотенузы, то он лежит против угла 30°.

⇒ ∠ОАЕ = 30°

• Сумма острых углов прямоугольного треугольника равна 90°.

⇒ ∠АОЕ = 90° - 30° = 60°

3. Рассмотрим ΔОАМ.

• Радиус, проведенный в точку касания, перпендикулярен касательной.

⇒ ΔОАМ - прямоугольный.

∠АОЕ = 60°, тогда ∠АМО = 90° - 60° = 30°

• Катет, лежащий против угла в 30°, равен половине гипотенузы.

⇒

4. ОА = ОК = R

⇒

⇒ OK : KM = 1 : 1

Или ОК = КМ.

Точка К делит отрезок МО в отношении 1 : 1.