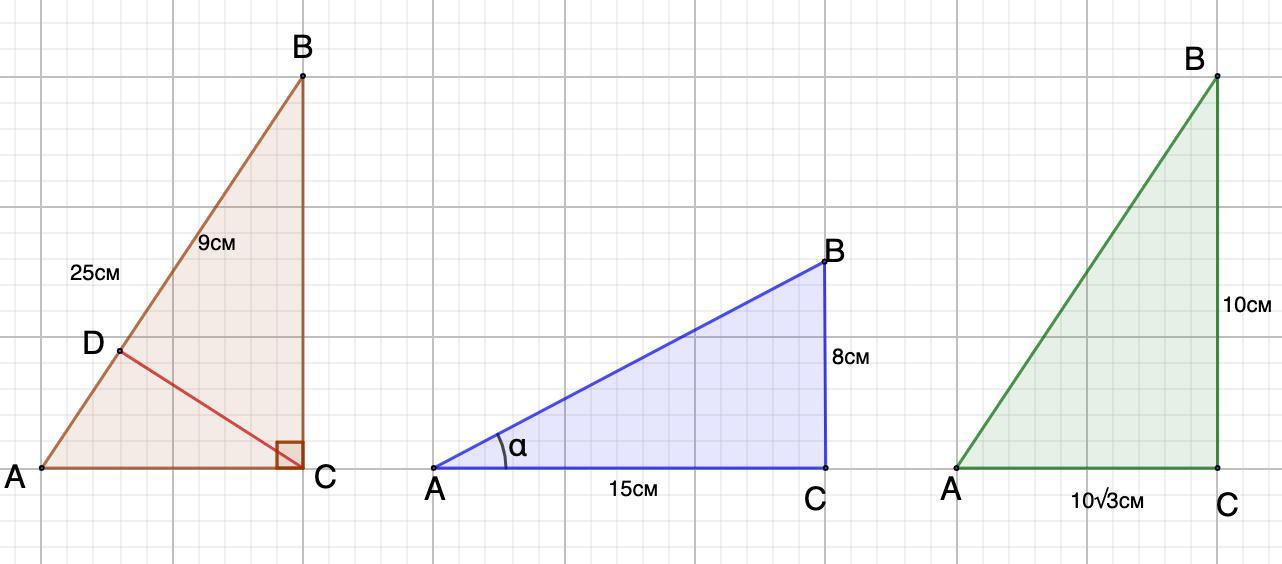
1
В прямоугольном треугольнике АВС , угол С прямой, СD – высота (рис.197 учебника).
АВ = 25 см, ВD= 9 см. Найдите СD, АС, ВС.
2
В прямоугольном треугольнике АВС , угол С =90о, катеты ВС = 8 см, АС = 15 см.
Найдите синус, косинус и тангенс угла А.
3
Найдите неизвестные стороны и углы прямоугольного треугольника, если его катеты
равны 10 и 10√3 см.Сделайте пожалуйста всё с дано и постраением плиз

Ответ:

1) СD = 12 см, АС = 20 см, ВС = 15 см.

2)

3) АВ = 20 см; ∠А = 30°; ∠В = 60°.

Объяснение:

1) Найдите СD, АС, ВС.

2) Найдите синус, косинус и тангенс угла А.

3) Найдите неизвестные стороны и углы прямоугольного треугольника.

1) Дано: ΔАВС - прямоугольный;

СD - высота;

АВ = 25 см, ВD= 9 см.

Найти: СD, АС, ВС.

Решение:

• Квадрат высоты прямоугольного треугольника, проведенной к гипотенузе, равен произведению проекций катетов на гипотенузу. Квадрат катета равен произведению гипотенузы и проекции этого катета на гипотенузу.

AD = AB - BD = 25 - 9 = 16 (см)

1. CD² = BD · AD = 9 · 16 = 144

CD = √144 = 12 (см)

2. AC² = AD · AB = 16 · 25 = 400

AC = √400 = 20 (см)

3. ВС² = DB · AB = 9 · 25 = 225

BC = √225 = 15 (см)

СD = 12 см, АС = 20 см, ВС = 15 см.

2) Дано: ΔАВС - прямоугольный;

ВС = 8 см; АС = 15 см.

Найти: синус, косинус и тангенс угла А.

Решение:

Пусть ∠А = α

• Синус угла - отношение противолежащего катета к гипотенузе.
• Косинус угла - отношение прилежащего катета к гипотенузе.
• Тангенс угла - отношение противолежащего катета к прилежащему.

Найдем гипотенузу по теореме Пифагора:

АВ² = ВС² + АС² = 64 + 225 = 289

АВ = √289 = 17 (см)

3) Дано: ΔАВС - прямоугольный;

∠С - прямой.

ВС = 10 см; АС = 10√3√ см.

Найти: АВ; ∠А; ∠В.

Решение:

1. АВ найдем по теореме Пифагора:

АВ² = ВС² + АС² = 100 + 300 = 400

АВ = √400 = 20 (см)

2. Найдем sin∠A, а затем ∠А.

3. Найдем ∠В.

Сумма острых углов прямоугольного треугольника равна 90°.

⇒ ∠В = 90° - ∠А = 90° - 30° = 60°

АВ = 20 см; ∠А = 30°; ∠В = 60°.