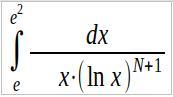[Высшая математика] Вычислить определённые интегралы: (см. изображение), где N = 18

Ответ:

(1-2¹⁸)/(3²*2¹⁹)=-262143/4 718 592

Пошаговое объяснение:

df(x)=f'(x)*dx⇒(1/х)*dx=d(㏑x)

введем замену ㏑х=t

тогда пределы интегрирования изменятся так:

нижний предел tнижн.= ㏑е=1; верхний tверхн.=㏑е²=2㏑е=2;

∫dt/t¹⁹=∫t⁻¹⁹dt=t⁻¹⁹⁺¹/18=1/(18*t¹⁸)

подставим по формуле Ньютона - Лейбница пределы интегрирования. получим1/(18*2¹⁸)-1/(18*1¹⁸)=(1/18)*(1/2¹⁸-1)==(1/18)*((1-2¹⁸)/2¹⁸)=(1-2¹⁸)/(18*2¹⁸)=

=(1-2¹⁸)/(3²*2¹⁹)=-262143/4 718 592