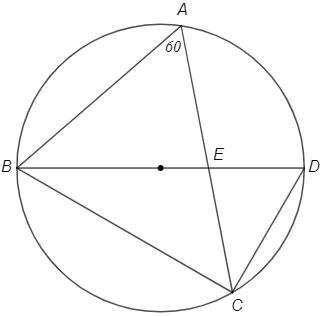
A, B, C и D — четыре точки, расположенные по часовой стрелке на окружности с центром в точке O, так что BD — диаметр окружности. AC и BD пересекаются в точке E, угол BAC = 60°, DE = 4 см и BE = 8 см. Найдите BC.

В сантиметрах

BD =BE+DE =8+4 =12

∠BDC =∠BAC =60° (вписанные углы, опирающиеся на одну дугу)

∠BCD =90° (опирается на диаметр)

∠CBD =90°-∠BDC =30°

CD =BD/2 =6 (катет против угла 30°)

BC =√(BD^2 -CD^2) =6√3 (см) (т Пифагора)

Или по т синусов, △BAC

BC/sinA =2R => BC =12*√3/2 =6√3 (см)